2015-06-14
782
| Границы интервалов | Средние интервалов х | Результат разноски | Итоги разноски | f×x | 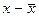 | 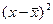 | f× |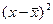
| 83–91 | ׀ | –36 | |||||
| 92–100 |  | –27 | |||||
| 101–109 | | –18 | |||||
| 110–118 |  | –9 | |||||
| 119–127 | S | ||||||
| 128–136 | £ | ||||||
| 137–145 | | ||||||
| 146–154 | ∟ | ||||||
| 155–163 | ׀ |
n=50;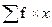 
=6150;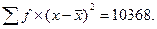 
6-й столбец показывает построчные разности между значениями x 2-го столбца и средним арифметическим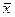 
.
7-й столбец – квадрат этих разностей.
8-й столбец показывает построчные произведения значений 4-го и 7-го столбцов. Суммирование величин этого столбца дает итог, необходимый для вычислений среднеквадратического отклонения.
Включение буквы f, означающей, насколько часто встречалась или другая величина, ничего не изменяет в формулах среднего арифметического и среднеквадратического отклонения. Поэтому формулы
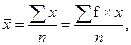
как и формулы
s=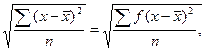 
вполне тождественны.
Остается показать, как вычисляются по формулам среднее арифметическое и среднеквадратическое отклонение. Обратимся к величинам, полученным в табл. 1:
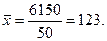
При составлении табл. 1 это число было заранее вычислено, без него нельзя было бы получить числовые значения 6, 7 и 8-го столбцов таблицы.
При обработке изучаемого ряда оказалось возможным применение параметрического методу визуально можно заметить, что распределение численностей приближается к нормальному.
Нормальное распределение обладает некоторыми весьма полезными для исследователя свойствами. Так, в границах 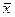± s находится примерно 68% всего ряда или всей выборки. В границах 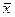± 20 находится примерно 95%, а в границах 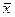± 3s – 99,7% выборки. В практике исследований часто берут границы 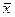± 2/3s. В этих границах при нормальном распределении будут находиться 50% выборки; распределение это симметрично, поэтому 25% окажутся ниже, а 25% выше границ 
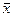± 2/3s. Все эти расчеты не требуют никакой дополнительной проверки при условии, что изучаемый ряд имеет нормальное распределение, а число элементов в нем велико, порядка нескольких сотен или тысяч.
Для рассматриваемого примера необходимо также вычислить коэффициент вариации по формуле:
%.
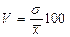В примере, который был рассмотрен выше,
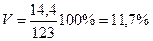
Выполнив все эти вычисления, психолог может представить информацию об изучении двигательной скорости с помощью примененной методики в шестых классах. Согласно результатам изучения в шестых классах, получены:
среднее арифметическое – 123;
среднеквадратическое отклонение –14,4;
коэффициент вариации – 11,7%.
Если значения изучаемого признака измерены в порядковой шкале, то в качестве меры центральной тенденции выступает медиана, а характеристикой диапазона варьирования выступает среднее квартальное отклонение.
Вот пример.
После проведения диагностических испытаний уровня умственного, развития учеников шестого класса все полученные данные были упорядочены, т.е. расположены в последовательности от меньшей величины к большей. Испытания проходили 18 учащихся. Буквами обозначены учащиеся, числами – полученные ими баллы по тесту, столбцы под буквами R – ранги (табл. 2).
Процедура ранжирования состоит в следующем. Все числа ряда в и последовательности получают по своим порядковым местам присваиваемые им ранги. Если какие-нибудь числа повторяются, то всем повторяющимся числам присваивается один и тот же ранг – средний из общей суммы занятых этими числами мест. Так, числу 28» в изучаемом ряду присвоен ранг «2». Затем следуют трижды повторяющиеся числа «39». На них приходятся занятые ими ранговые места «3», «4», «5». Поэтому этим числам присваивается один и тот же средний ранг, в данною случае – «4». Поскольку места до 5 включительно заняты, то следующее число получает ранг «6» и т.д.
Таблица 2
