Нестационарные явления переноса в газах

Рассмотренные нами явления переноса
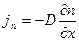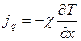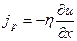: : (1)

представляли собой стационарные процессы, так как ни плотности потоков, ни градиенты соответствующих параметров не зависели от времени. Такие стационарные процессы наблюдаются в природе: например, распространение теплоты от Солнца. Однако существует множество ситуаций, когда условие назависимости от времени не выполняется, и протекающие процессы являются нестационарными. Примером такого нестационарного процесса является диффузия паров нашатырного спирта в замкнутой колбе, где индикатором диффузии служит полоска бумаги, смоченная фенолфталеином. Рассмотрим специфику нестационарных процессов и возможности их описания.

§ 10. Нестационарная диффузия.

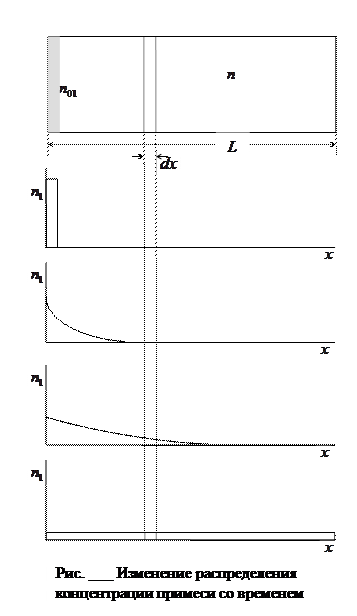
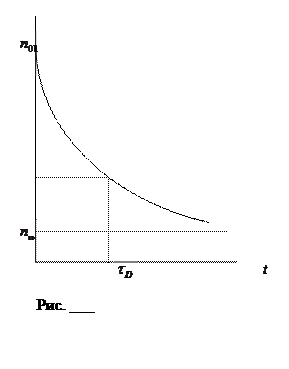
Рассмотрим замкнутую трубку длиной L, заполненную некоторым газом с концентрацией n. Введем в трубку с одного конца примесь с концентрацией n₀₁. Если не поддерживать между концами трубки постоянного градиента концентрации примеси, то в результате теплового хаотического движения через некоторое время система релаксирует к состоянию равновесия, т.е. примесь равномерно распределится по всему объему трубки (рис. ___).

Рассмотрим подробнее, какова закономерность изменения концентрации примеси со временем вдоль оси x - 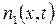. Выделим в трубке объем площадью 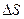и длиной 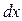. Так как введенная в трубку примесь распространяется от одного конца к другому, ее концентрация всюду является функцией времени:

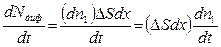, (2)

где 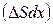- выделенный объем трубки. С другой стороны, изменение числа диффундирующих частиц со временем в выделенном объеме 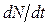будет обусловлено тем, что потоки через левую и правую площадки будут разными, т.е.

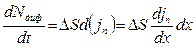. (3)

тогда, приравняв правые части выражений (2) и (3), получим

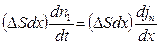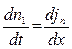, или . (4)

Подставляя в равенство (4) выражение для 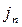из закона Фика,

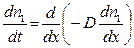
Получим уравнение для нестационарной диффузии

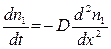. (5)

Проанализируем это уравнение: пусть длина трубки - 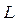, в начальный момент времени концентрация примеси у левого конца трубки - 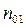, а у правого – 0, тогда 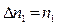и 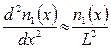. С учетом этих допущений

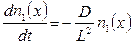. (6)

Разделив переменные 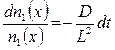и проинтегрировав это выражение, получим

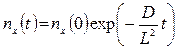. (7)

В точке 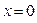при 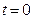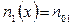, а при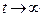 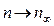, тогда выражение (7) принимает вид

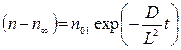. (8)

Величину 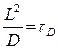- называют временем макроскопической релаксации системы, т.е. временем установления равновесного состояния в данной макросистеме. Применительно к нестационарной диффузии 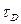- это время, в течение которого концентрация во всех точках выравнивается и в объеме устанавливается термодинамическое равновесие.

Так как 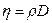, то 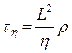- характеризует время затухания направленных движений в газах после устранения источников этих движений, и уравнение нестационарной вязкости будет иметь вид

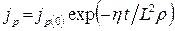. (9)

Так как æ = 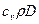, то τ_æ = 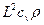/ æ, и уравнение нестационарной теплопроводности будет иметь вид

j_Q = j_Q(0) exp(-æt/L²c_vr). (10)

Таким образом, после прекращения внешних воздействий все изменения, связанные с этими воздействиями, будут затухать с характеристическим временем затухания 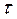по экспоненциальному закону. Макроскопическое время установления термодинамического равновесия в системе 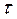имеет глубокий физический смысл: если изменения в системе будут происходить в течение времени Dt» 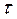, то такой процесс можно рассматривать как квазиравновесный, если же Dt £ 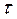, то процесс нельзя считать квазиравновесным.