БИЛЕТ ОБЛАСТНОЙ ОЛИМПИАДЫ ПО МАТЕМАТИКЕ
ЗАДАЧА 1. Два самолёта движутся прямолинейно и равномерно. Неизвестно, являются ли их траектории пересекающимися или скрещивающимися прямыми. На самолётах вышли из строя системы, определяющие скорость и координаты в пространстве. Работает только радар, измеряющий расстояние до другого объекта в воздухе. Было сделано 3 измерения через равные промежутки времени (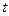 = 0,1,2 сек.), зафиксированы расстояния
= 0,1,2 сек.), зафиксированы расстояния 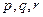 . (причём
. (причём 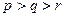 , т.к. они сближаются). Вывести формулу для бортовой системы предотвращения столкновений, которая по этим параметрам вычислит минимальное расстояние между самолётами, которое будет достигнуто, если будет продолжено прямолинейное и равномерное движение.
, т.к. они сближаются). Вывести формулу для бортовой системы предотвращения столкновений, которая по этим параметрам вычислит минимальное расстояние между самолётами, которое будет достигнуто, если будет продолжено прямолинейное и равномерное движение.
ЗАДАЧА 2. Открывающаяся секция пластикового окна - прямоугольник со сторонами 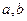 , причём , причём 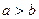 . При вертикальном открывании секция держится на металлическом штыре длины равной . При вертикальном открывании секция держится на металлическом штыре длины равной 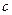 ( (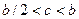 ), который с одной стороны закреплён в углу неподвижной части, а с другой стороны скользит ровно до середины движущейся секции. Вычислить максимальный угол, на который открывается окно. ), который с одной стороны закреплён в углу неподвижной части, а с другой стороны скользит ровно до середины движущейся секции. Вычислить максимальный угол, на который открывается окно.
| 
|
ЗАДАЧА 3. Вывести формулу расстояния по поверхности планеты между двумя городами, географические координаты которых 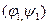 и
и 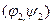 , где
, где 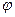 - широта (от
- широта (от
-900 до 900), 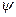 - долгота (от 00 до 3600). Планету считать идеальным шаром радиуса R.
- долгота (от 00 до 3600). Планету считать идеальным шаром радиуса R.
ЗАДАЧА 4. Найти, какую максимальную долю объёма может занимать прямой круговой конус, вписанный в шар радиуса 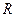 .
.
ЗАДАЧА 5. Для функции 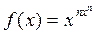 на множестве
на множестве 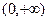 при каждом
при каждом 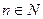 существует точка экстремума
существует точка экстремума 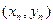 . Найти предельную точку этой последовательности:
. Найти предельную точку этой последовательности: 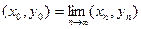 .
.
ЗАДАЧА 6. На прямой 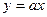 при любом параметре
при любом параметре 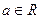 есть точка, ближайшая к точке (С,0). Найти неявное уравнение кривой, которую образуют все такие точки при
есть точка, ближайшая к точке (С,0). Найти неявное уравнение кривой, которую образуют все такие точки при 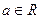 .
.
Желаем успеха! На странице vk.com/tusur120415 решения и результаты проверки будут в воскресенье вечером.
2015 1 курс
ЗАДАЧА 1. Два самолёта движутся прямолинейно и равномерно. Неизвестно, являются ли их траектории пересекающимися или скрещивающимися прямыми. На самолётах вышли из строя системы, определяющие скорость и координаты в пространстве. Работает только радар, измеряющий расстояние до другого объекта в воздухе. Было сделано 3 измерения через равные промежутки времени (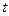 = 0,1,2 сек.), зафиксированы расстояния
= 0,1,2 сек.), зафиксированы расстояния 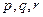 . (причём
. (причём 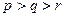 , т.к. они сближаются). Вывести формулу для бортовой системы предотвращения столкновений, которая по этим параметрам вычислит минимальное расстояние между самолётами, которое будет достигнуто, если будет продолжено прямолинейное и равномерное движение.
, т.к. они сближаются). Вывести формулу для бортовой системы предотвращения столкновений, которая по этим параметрам вычислит минимальное расстояние между самолётами, которое будет достигнуто, если будет продолжено прямолинейное и равномерное движение.
РЕШЕНИЕ ЗАДАЧИ 1.
Пусть 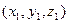 и
и 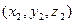 координаты первого и второго объекта в начальный момент времени,
координаты первого и второго объекта в начальный момент времени, 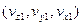 и
и 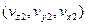 - векторы скорости этих объектов, тогда квадрат расстояния между ними как функция от времени
- векторы скорости этих объектов, тогда квадрат расстояния между ними как функция от времени 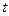 :
:
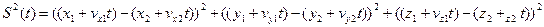
После раскрытия скобок получится квадратный трёхчлен вида 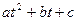 . Известно, что парабола полностью определяется своими значениями в трёх различных точках. Таким образом, для 3 различных измерений расстояния можно определить расстояние между объектами в любой последующий момент времени, а значит, вычислить минимум расстояния (и время, в которое он будет достигаться). Измеренные расстояния в моменты времени 0,1,2 сек. равны соответственно
. Известно, что парабола полностью определяется своими значениями в трёх различных точках. Таким образом, для 3 различных измерений расстояния можно определить расстояние между объектами в любой последующий момент времени, а значит, вычислить минимум расстояния (и время, в которое он будет достигаться). Измеренные расстояния в моменты времени 0,1,2 сек. равны соответственно 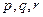 , тогда коэффициенты в уравнении квадрата расстояния между объектами могут быть вычислены из системы линейных уравнений с неизвестными
, тогда коэффициенты в уравнении квадрата расстояния между объектами могут быть вычислены из системы линейных уравнений с неизвестными 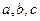 (для
(для 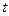 =0,1,2 соответственно):
=0,1,2 соответственно):
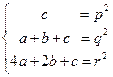
Из первого выразим 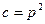 , тогда система сводится к системе двух уравнений:
, тогда система сводится к системе двух уравнений:
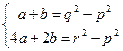
Решая эту систему методом Гаусса, получаем:
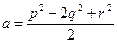 ,
, 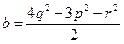 .
.
Теперь известны все коэффициенты функции 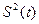 , можно вычислить время, при котором достигается минимальное сближение. Вершина параболы имеет абсциссу
, можно вычислить время, при котором достигается минимальное сближение. Вершина параболы имеет абсциссу 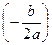 , поэтому
, поэтому 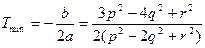 . Квадрат минимального расстояния, достигаемый в указанный момент времени:
. Квадрат минимального расстояния, достигаемый в указанный момент времени:  =
= 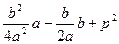 =
= 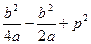 =
= 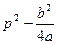 =
= 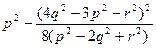 . Тогда
. Тогда 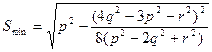 .
.
Ответ: 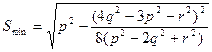 .
.
Примечание. Если правильно найдено 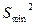 , но в конце забыт квадратный корень, оценить 9 баллов.
, но в конце забыт квадратный корень, оценить 9 баллов.
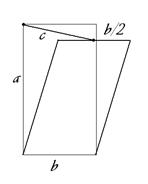
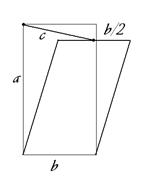
ЗАДАЧА 2. Открывающаяся секция пластикового окна - прямоугольник со сторонами 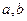 , причём , причём 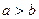 . При вертикальном открывании секция держится на металлическом штыре длины равной . При вертикальном открывании секция держится на металлическом штыре длины равной 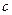 ( (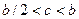 ), который с одной стороны закреплён в углу неподвижной части, а с другой стороны скользит ровно до середины движущейся секции. Вычислить максимальный угол, на который открывается окно. ), который с одной стороны закреплён в углу неподвижной части, а с другой стороны скользит ровно до середины движущейся секции. Вычислить максимальный угол, на который открывается окно.
| 
|
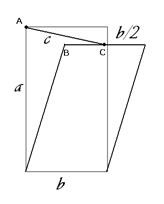
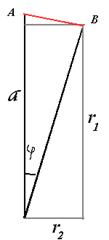
РЕШЕНИЕ ЗАДАЧИ 2.
На чертеже 2 видно, что 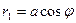 , , 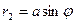 . Вычислим по теореме Пифагора расстояние от угловой точки неподвижной части до середины открывающейся секции в зависимости от . Вычислим по теореме Пифагора расстояние от угловой точки неподвижной части до середины открывающейся секции в зависимости от 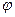 . В проекции на плоскость, перпендикулярную повороту, это расстояние . В проекции на плоскость, перпендикулярную повороту, это расстояние 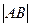 , составляющее , составляющее 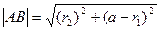 , ,
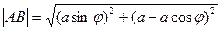 При этом также видно, что
При этом также видно, что 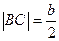 . .
|  
|
Тогда 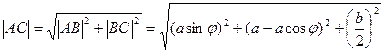
Но при этом по условию, 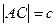 , поэтому:
, поэтому: 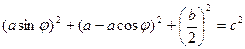 .
.
Далее преобразуем это выражение, чтобы выразить 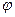 .
.
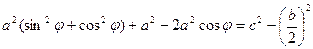 ,
, 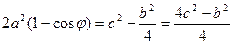 ,
,
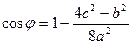 ,
, 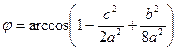 =
= 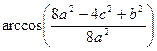 .
.
Ответ: 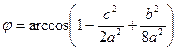 .
.
ЗАДАЧА 3. Вывести формулу расстояния по поверхности планеты между двумя городами, географические координаты которых 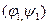 и
и 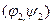 , где
, где 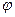 - широта (от -900 до 900),
- широта (от -900 до 900), 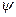 - долгота (от 00 до 3600). Планету считать идеальным шаром радиуса R.
- долгота (от 00 до 3600). Планету считать идеальным шаром радиуса R.
РЕШЕНИЕ ЗАДАЧИ 3.
Найдём формулы перехода от декартовых координат к географическим.
Проекция на ось Oz соответствует sin широты, 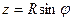 . Тогда проекция на плоскость Oxy есть
. Тогда проекция на плоскость Oxy есть 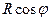 , а она проецируется ещё на оси x,y.
, а она проецируется ещё на оси x,y.
Имеем 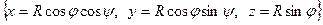 .
.
(Как сферические координаты, только 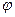 отмеряется от экватора, а не северного полюса).
отмеряется от экватора, а не северного полюса).
Теперь проведём два радиус-вектора к двум данным точкам планеты из её центра.
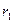 =
= 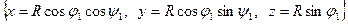 .
.
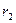 =
= 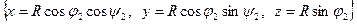 .
.
Скалярное произведение равно произведению модулей на косинус угла. Таким образом, угол равен 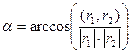 . Также верно
. Также верно 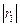 =
= 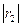 =
= 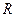 , т.к. обе точки расположены на поверхности планеты.
, т.к. обе точки расположены на поверхности планеты.
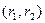 =
= 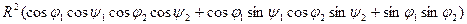 =
=
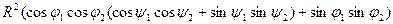 =
=
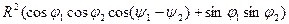 .
.
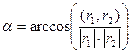 =
= 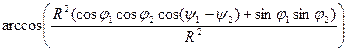 =
=
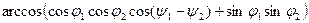 - угол между векторами, проведёнными из центра планеты к двум точкам с данными географическими координатами. Чтобы найти расстояние, нужно этот угол умножить на радиус планеты, то есть
- угол между векторами, проведёнными из центра планеты к двум точкам с данными географическими координатами. Чтобы найти расстояние, нужно этот угол умножить на радиус планеты, то есть 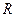 .
.
В итоге  .
.
(Если угол максимален, 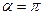 , получается
, получается 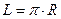 , половина длины окружности).
, половина длины окружности).
Ответ.  .
.
ЗАДАЧА 4. Найти, какую максимальную долю объёма может занимать прямой круговой конус, вписанный в шар радиуса 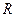 .
.
РЕШЕНИЕ ЗАДАЧИ 4.
Объём шара равен, как известно, 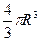 . Для вписанного в шар конуса, высота
. Для вписанного в шар конуса, высота 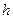 и радиус
и радиус 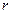 взаимосвязаны между собой. Расстояние от центра основания конуса до центра шара есть
взаимосвязаны между собой. Расстояние от центра основания конуса до центра шара есть 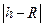 (см.чертёж - вид сбоку, на чертеже это ОС). Отрезок ВС на чертеже равен
(см.чертёж - вид сбоку, на чертеже это ОС). Отрезок ВС на чертеже равен 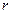 - радиусу основания конуса. Далее, по теореме Пифагора (ОС)2+(ВС)2 = (ОВ)2.
- радиусу основания конуса. Далее, по теореме Пифагора (ОС)2+(ВС)2 = (ОВ)2.
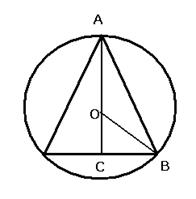
То есть, 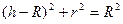 , следовательно,
, следовательно, 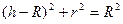 ,
, 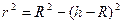 ,
,
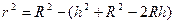 ,
, 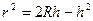 . По известным формулам, объём конуса равен
. По известным формулам, объём конуса равен 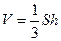 , а площадь основания
, а площадь основания 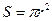 , тогда
, тогда 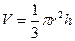 ,
, 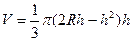 =
= 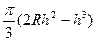 .
.
Найдём экстремум по 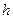 .
.
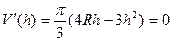 ,
, 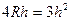 ,
, 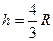 . При этом значении объём конуса равен
. При этом значении объём конуса равен 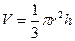 =
= 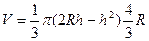 =
= 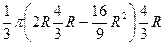 =
= 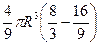 =
= 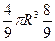 =
= 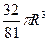 .
.
Нужно найти отношение объёма конуса к объёму шара, поэтому поделим друг на друга объёмы этих тел: 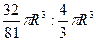 =
= 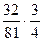 =
= 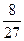 .
.
ОТВЕТ. Максимальная доля объёма, занимаемая вписанным конусом в шаре, 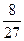 .
.
ЗАДАЧА 5. Для функции 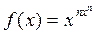 на множестве
на множестве 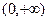 при каждом
при каждом 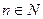 существует точка экстремума
существует точка экстремума 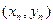 . Найти предельную точку этой последовательности:
. Найти предельную точку этой последовательности: 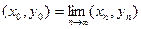 .
.
РЕШЕНИЕ ЗАДАЧИ 5.
Необходимо сначала найти экстремум для произвольного n.
Прологарифмируем исходное выражение: 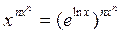 =
= 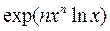 .
.
Тогда 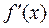 =
= 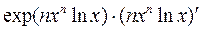 =
= 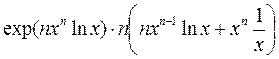 =
= 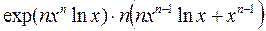 =
=
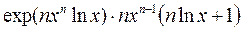 . Обращаться в 0 на правой полуоси может только множитель
. Обращаться в 0 на правой полуоси может только множитель 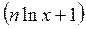 , поэтому экстремум достигается при
, поэтому экстремум достигается при 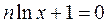 , то есть
, то есть
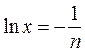 ,
, 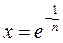 . Итак, для n получили
. Итак, для n получили 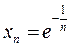 . При этом ордината
. При этом ордината
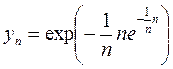 ,
, 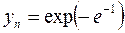 =
= 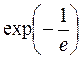 =
= 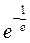 .
.
При этом оказалось, что ордината не зависит от n.
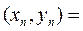
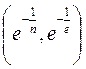 . Предел нужно вычислить только по первой координате, так как вторая есть константа.
. Предел нужно вычислить только по первой координате, так как вторая есть константа. 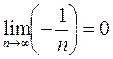 поэтому
поэтому 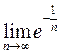 =
= 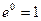 . ОТВЕТ. Точка
. ОТВЕТ. Точка 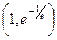 .
.
Ниже для сведения показаны графики этих функций. Экстремум смещается вправо при увеличении n, но остаётся на той же самой высоте.
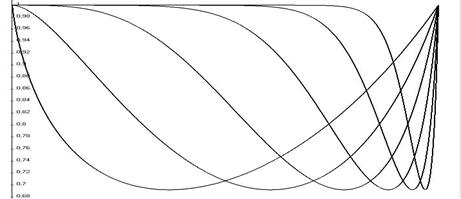
ОТВЕТ. Предельной является точка 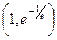 .
.
ЗАДАЧА 6. На прямой 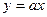 при любом параметре
при любом параметре 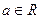 есть точка, ближайшая к точке (С,0). Найти неявное уравнение кривой, которую образуют все такие точки при
есть точка, ближайшая к точке (С,0). Найти неявное уравнение кривой, которую образуют все такие точки при 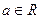 .
.
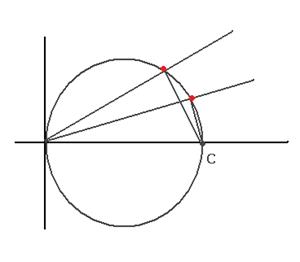
РЕШЕНИЕ ЗАДАЧИ 6.
Пусть точка является ближайшей к (С,0). Тогда вектор 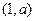 , расположенный на прямой, перпендикулярен вектору, соединяющему точку
, расположенный на прямой, перпендикулярен вектору, соединяющему точку 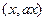 с точкой
с точкой 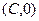 , то есть вектору
, то есть вектору
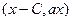 . Скалярное произведение векторов
. Скалярное произведение векторов 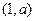 и
и 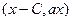 равно 0, то есть
равно 0, то есть
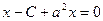 . Отсюда можно найти абсциссу точки, которая является ближайшей к указанной.
. Отсюда можно найти абсциссу точки, которая является ближайшей к указанной. 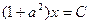 ,
, 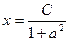 . Тогда
. Тогда 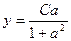 . Это параметрические уравнения кривой. Чтобы найти неявное уравнение кривой, нужно устранить зависимость от параметра, то есть выразить
. Это параметрические уравнения кривой. Чтобы найти неявное уравнение кривой, нужно устранить зависимость от параметра, то есть выразить 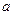 из одного уравнения и подставить во второе. Из первого уравнения:
из одного уравнения и подставить во второе. Из первого уравнения: 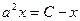 ,
, 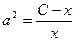 ,
, 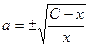 .
.
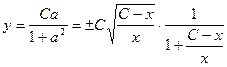 =
= 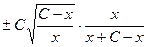 =
= 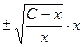 =
= 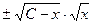
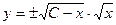 тогда
тогда 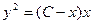 ,
, 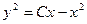 ,
, 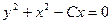 , выделим полный квадрат:
, выделим полный квадрат: 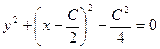 ,
, 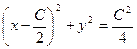 .
.
Таким образом, кривая, состоящая из точек, являющихся ближайшими к (С,0), есть окружность с центром в точке 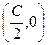 радиуса
радиуса 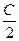 .
.
ОТВЕТ. 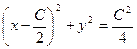 окружность с центром в точке
окружность с центром в точке 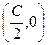 радиуса
радиуса 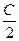 .
.
 2015-06-16
2015-06-16 541
541







