2015-06-04
956
Ошибки статистического наблюдения.
Информация, полученная в ходе статистического наблюдения может не отвечать действительности, а расчетные значения показателей не соответствовать фактическим значениям.
Расхождение между расчетным значением и фактическим называется ошибкой наблюдения.
В зависимости от причин возникновения различают ошибки регистрации и ошибки репрезентативности. Ошибки регистрации характерны как для сплошного, так и для несплошного наблюдения, а ошибки репрезентативности — только для несплошного наблюдения. Ошибки регистрации, как и ошибки репрезентативности, могут быть случайными и систематическими.
Ошибки регистрации — представляют собой отклонения между значением показателя, полученного в ходе статистического наблюдения, и его фактическим значением. Ошибки регистрации бывают случайными (результат действий случайных факторов — перепутаны строки например) и систематическими (проявляются постоянно).
Ошибки репрезентативности — возникают, когда отобранная совокупность недостаточно точно воспроизводит исходную совокупность. Характерны для несплошного наблюдения и заключаются в отклонении величины показателя исследуемой части совокупности от его величины в генеральной совокупности.
Случайные ошибки — являются результатом действия случайных факторов.
Систематические ошибки — всегда имеют одинаковую направленность к увеличению или уменьшению показателя по каждой единице наблюдения, вследствие чего значение показателя по совокупности в целом будет включать накопленную ошибку.
Способы контроля:
§ Счетный (арифметический) — проверка правильности арифметического расчета.
§ Логический — основан на смысловой взаимосвязи между признаками.
Ошибка выборочного наблюдения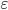 
есть разность между значением параметра в генеральной совокупности и ее выборочным значением. Для среднего значения количественного признака она равна: 
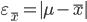, а для доли (альтернативного признака) — 
.
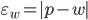Ошибки выборки свойственны только выборочным наблюдениям. Чем больше эти ошибки, тем больше эмпирическое распределение отличается от теоретического. Параметры эмпирического распределения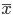 
и 
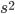являются случайными величинами, следовательно, ошибки выборки также являются случайными величинами, могут принимать для разных выборок разные значения и поэтому принято вычислять среднюю ошибку.
Средняя ошибка выборки есть величина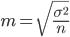 
, выражающая среднее квадратическое отклонение выборочной средней от математического ожидания. Эта величина при соблюдении принципа случайного отбора зависит прежде всего от объема выборки 
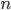и от степени варьирования признака: чем больше 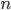и чем меньше вариация признака (следовательно, и значение 
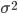), тем меньше величина средней ошибки выборки 
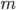. Соотношение между дисперсиями генеральной и выборочной совокупностей выражается формулой:
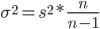
т.е. при достаточно больших 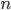можно считать, что 
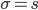. Средняя ошибка выборки показывает возможные отклонения параметра выборочной совокупности от параметра генеральной. В табл. 9.2 приведены выражения для вычисления средней ошибки 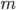выборки при разных методах организации наблюдения.
Таблица 9.2 Средняя ошибка (m) выборочных средней и доли для разных видов выборки
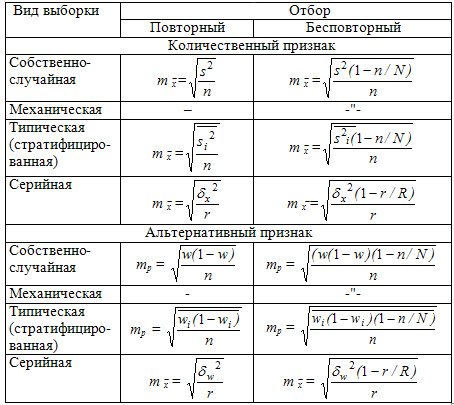
Где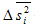 
- средняя из внутригрупповых выборочных дисперсий для непрерывного признака;
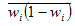- средняя из внутригрупповых дисперсий доли;
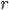— число отобранных серий, 
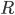— общее число серий;
,
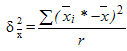где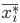 
— средняя 
-й серии;
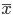— общая средняя по всей выборочной совокупности для непрерывного признака;
,
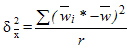где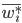 
— доля признака в -й серии;
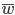— общая доля признака по всей выборочной совокупности.
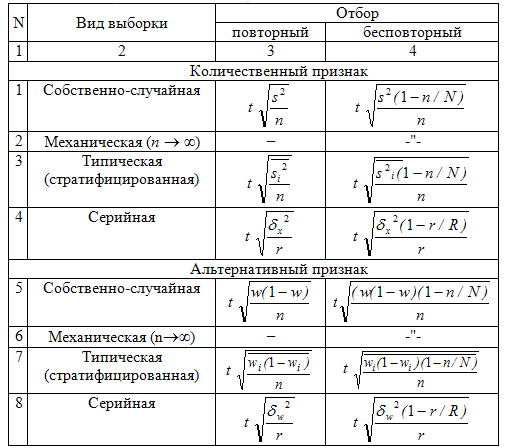
В табл. 9.3 приведены формулы для вычисления предельной ошибки выборки.
Таблица 9.3 Предельная ошибка (D) выборки для средней и доли (р) для разных видов выборочного наблюдения
