В математике принято произвольную первообразную функцию для заданной функции  называть неопределенным интегралом от
называть неопределенным интегралом от  и обозначать его в виде
и обозначать его в виде
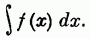
Таким образом, если 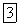 есть некоторая вполне определенная первообразная для
есть некоторая вполне определенная первообразная для  то неопределенный интегралот
то неопределенный интегралот 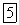 равен
равен
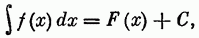
где С — произвольная постоянная.
Отметим еще, что если функция  дана на отрезке
дана на отрезке  первообразная и х — точка отрезка
первообразная и х — точка отрезка  то на основанииформулы Ньютона — Лейбница можно написать
то на основанииформулы Ньютона — Лейбница можно написать
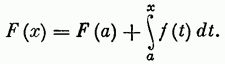
Таким образом интеграл, стоящий в правой части этого равенства, только на постоянную  отличается от функции
отличается от функции  первообразной для
первообразной для  . В таком случае этот интеграл, если его рассматривать как функцию верхнего предела х (при переменном
. В таком случае этот интеграл, если его рассматривать как функцию верхнего предела х (при переменном  есть некоторая вполне определенная первообразная для
есть некоторая вполне определенная первообразная для  и, следовательно, неопределенный интеграл от
и, следовательно, неопределенный интеграл от  можно записать еще в следующем виде:
можно записать еще в следующем виде:
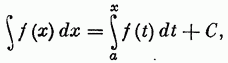
где С — произвольная постоянная.
Приведем основную таблицу неопределенных интегралов, составленную непосредственно из соответствующей таблицы производных (см. § 6):
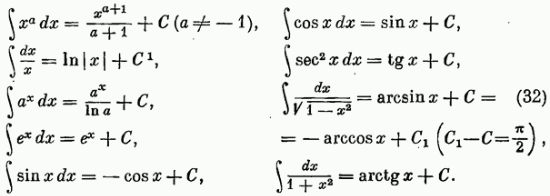
Общие свойства неопределенных интегралов также выводятся на основании соответствующих свойств производных. Например, из правила дифференцирования суммы получаем формулу
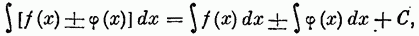
а из соответствующего правила, выражающего, что постоянный множитель к можно выносить за знакпроизводной, получим
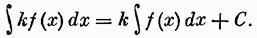
Таким образом,
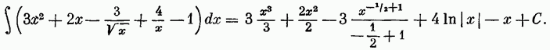
Существует ряд методов вычисления неопределенных интегралов. Остановимся на одном из них, а именно на методе подстановки или замены переменной, который основан на  справедливости следующего равенства:
справедливости следующего равенства:
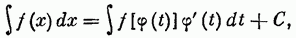
Приведем несколько примеров на применение метода подстановки
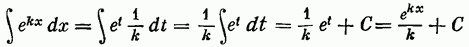
(подстановка  откуда к
откуда к 
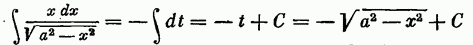
подстановка  откуда
откуда 
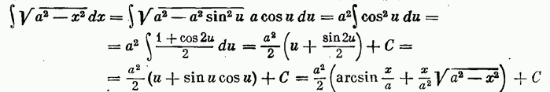
(подстановка 
 2015-06-16
2015-06-16 121
121






