И так, все круги в этой модели – женские. Существует тринадцать способов наложения мужской энергии - иными словами, прямых линий - на эти тринадцать кругов. Если наложить на эту модель прямые линии всеми тринадцатью способами, то получится тринадцать моделей, которые, вместе с Яйцом жизни и тором, создают в бытии всё. Яйцо Жизни, тор и плод Жизни, эти три модели в совокупности создают в бытии всё без исключения – по крайней мере, мне не удалось найти ни одного исключения. Я дам вам то, чему научился; Ясно, что всё я вам показать не могу, но я покажу вам достаточно, чтобы убедить вас в том, что это правда. Я назову эти информационные системы. С моделью Плода Жизни связаны тринадцать информационных систем. Каждая система производит обширный и разнообразный объём знаний. Я покажу вам только четыре из них. Думаю, этого достаточно.
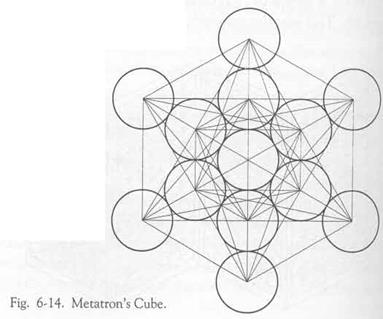 Простейшая система проявляется простым соединением всех центров всех кругов прямыми линиями. Если вы решили провести прямые линии на этой модели, то, вероятно, около 90 процентов из вас прежде всего решит соединить ими все центры. Если вы это проделаете, то получите модель (Рис.6-14), которая во всей вселенной – повсюду – известна как Куб Метатрона. Это одна из наиболее важных информационных систем во вселенной, одна из основных моделей творения бытия.
Простейшая система проявляется простым соединением всех центров всех кругов прямыми линиями. Если вы решили провести прямые линии на этой модели, то, вероятно, около 90 процентов из вас прежде всего решит соединить ими все центры. Если вы это проделаете, то получите модель (Рис.6-14), которая во всей вселенной – повсюду – известна как Куб Метатрона. Это одна из наиболее важных информационных систем во вселенной, одна из основных моделей творения бытия.
П латоновы Тела
К аждый, изучавший священную геометрию или даже просто обычную геометрию, знает, что существуют пять уникальных форм, и для понимания как священной, так и обычной геометрии они являются решающими. Их именуют Платоновыми телами (Рис.6-15).
П латоново тело определяется некоторыми характеристиками. Прежде всего, все грани его имеют одинаковый размер. Например, куб, самое известное из Платоновых тел, имеет каждой своей гранью квадрат, и все его грани - одинакового размера. Второе, все рёбра Платонового тела имеют одинаковую длину; все рёбра куба – одной длины. Третьее: все внутренние углы между гранями имеют одинаковую величину. В случае куба, этот угол равен 90 градусам. И четвёртое: если Платоново тело поместить внутрь сферы (правильной формы), то все вершины его будут касаться поверхности сферы. Таким определениям, кроме куба (А), отвечают только четыре формы, обладающие всеми этими характеристиками. Вторым будет тетраэдр (В) (тетра означает «четыре») – это полиэдр, имеющий четыре грани, все - равносторонние треугольники, одинаковую длину рёбер и одинаковый угол, и – все вершины касаются поверхности сферы. Другая простая форма – это октаэдр (С) (окта значит «восемь»), все восемь граней представляют собой равносторонние треугольники одинакового размера, длина рёбер и углов одинакова, и все вершины касаются поверхности сферы.
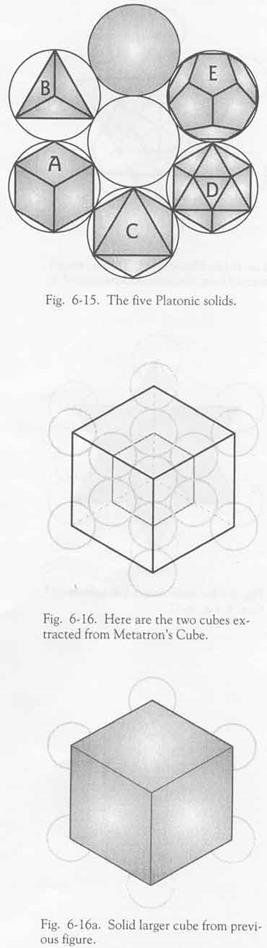 Остальные два Платоновых тела немного сложнее. Один называется икосаэдром (D) - значит, он имеет 20 граней, имеющих вид равносторонних треугольников при одинаковой длине рёбер и углов; все его вершины тоже касаются поверхности сферы. Последний называется пентагональным додeкаэдром (Е) (додэка - это 12), гранями которого являются 12 пентагонов (пятиугольники) при одинаковой длине рёбер и одинаковых углах; все его вершины касаются поверхности сферы.
Остальные два Платоновых тела немного сложнее. Один называется икосаэдром (D) - значит, он имеет 20 граней, имеющих вид равносторонних треугольников при одинаковой длине рёбер и углов; все его вершины тоже касаются поверхности сферы. Последний называется пентагональным додeкаэдром (Е) (додэка - это 12), гранями которого являются 12 пентагонов (пятиугольники) при одинаковой длине рёбер и одинаковых углах; все его вершины касаются поверхности сферы.
Е сли вы – инженер или архитектор, то вы изучали эти пять форм в колледже, хотя бы поверхностно, потому что они являются базовыми структурами.
 2015-06-16
2015-06-16 438
438








