2015-06-16
495
1. Условие (3.8 а) можно записать в векторной форме: ∇ xL (x *, λ0*, λ0*) = 0.
2. Система (3.8) содержит n + m уравнений с n + m + 1 неизвестными λ0*, λ*= (λ1*, …, λ m *) T, x * = (x 1*, …, xn *) T. Точки х *, удовлетворяющие системе при некоторых λ0*, λ*, называются условно-стационарными.
3. При решении задач проверка условия регулярности затруднена, так как точка х * заранее не известна. Поэтому, как правило, рассматриваются два случая: λ0*= 0 и λ0*≠ 0. Если λ0*≠ 0, в системе (3.8 а) полагают λ0*= 1. Это эквивалентно делению системы уравнений (3.8 а) на λ0*и замене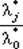 
на λ j *. При этом обобщенная функция Лагранжа становится классической, а сама система (3.8) имеет вид
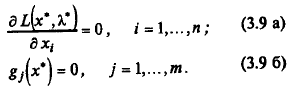
Здесь число уравнений равно числу неизвестных.
4. Система (3.9) отражает тот факт, что антиградиент целевой функции в регулярной точке экстремума х * является линейной комбинацией градиентов ограничений. Действительно, с учетом (3.3) можно переписать условие (3.9 а) в форме
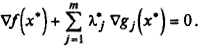
Отсюда
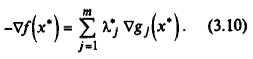
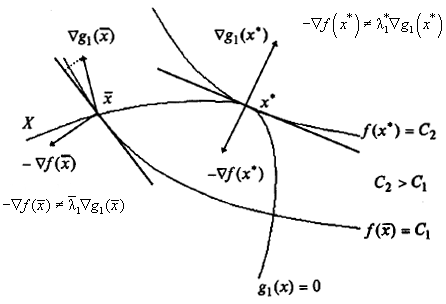
Рис. 3.2
Точка х * условного экстремума (максимума) является точкой касания линии уровня целевой функции и кривой, описывающей ограничение (рис. 3.2). В точке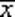 
возможно движение вдоль ограничения, связанное с увеличением функции.
|
|
|
5. Точка экстремума, удовлетворяющая системе (3.8) при λ0*≠ 0, называется регулярной, а при λ0*= 0 — нерегулярной. Случай λ0*= 0 отражает вырожденность ограничений. При этом в обобщенной функции Лагранжа исчезает член; содержащий целевую функцию, а в необходимых условиях экстремума не используется информация, представляемая градиентом целевой функции.
6. Условие допустимости решения, являющееся следствием постановки задачи (3.7), включено в (3.8), (3.9) для удобства формирования алгоритма решение задачи.
Утверждение 3.2 (необходимые условия экстремума второго порядка).
Пусть х * — регулярная точка минимума (максимума) в задаче (3.7) и имеется решение (х *, λ *). Тогда второй дифференциал классической функции Лагранжа, вычисленный в точке (х *, λ *), неотрицателен (неположителен):
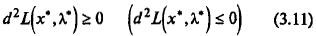
для всех d х ∈ Rn таких, что
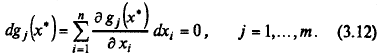
Утверждение 3.3 (достаточные условия экстремума).
Пусть имеется точка (х *, λ *), удовлетворяющая системе (3.9). Если в этой точке d 2 L (х *, λ *) > 0 (d 2 L (х *, λ *) < 0) для всех ненулевых dx ∈ R n таких, что
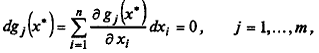
то точка х * является точкой локального минимума (максимума) в задаче (3.7).
Замечание 3.2. Достаточные и необходимые условия экстремума второго порядка проверяются в условно-стационарных точках, которые удовлетворяют системе (3.8) при λ0*≠ 0 или системе (3.9), так как для практики безусловно представляет интерес случай, когда в функции Лагранжа присутствует целевая функция, экстремум которой ищется.
|
|
|
