Критерий Гурвица. Это самый универсальный критерий, который позволяет управлять степенью «оптимизма - пессимизма» ЛПР

Это самый универсальный критерий, который позволяет управлять степенью «оптимизма - пессимизма» ЛПР. Введем некоторый коэффициент a, который назовем коэффициентом доверия или коэффициентом оптимизма. Этот коэффициент можно интерпретировать как вероятность, с которой произойдет наилучший

для ЛПР исход. Исходя из этого, наихудший вариант можно ожидать с

рассчитывает на благоприятный для него исход. Если вероятности

благоприятной и неблагоприятной ситуации для ЛПР равны, то следует принять a =0,5

Для реализации критерия определяются наилучшие 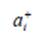и наихудшие 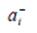значение каждой альтернативе по формулам

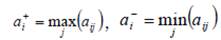
Далее, вычисляются функции полезности по формуле:

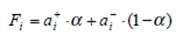
Выбирается та альтернатива, для которой функция полезности максимальна.

Предположим, что для нашего примера ЛПР достаточно уверен в положительном результате и оценивает вероятность максимального

успеха в a =0,7. Тогда:

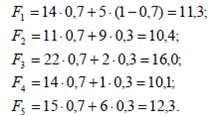
В соответствии с расчетами ЛПР следует выбрать альтернативу А 3. Если же, например, ЛПР не очень уверен в положительном исходе и расценивает его вероятность порядка a =0,2, то функции полезности равны:

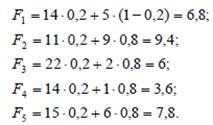
Видно, что в этом случае следует принять А 2, для которого функция полезности максимальна.

Следует отметить, что при a =0, критерий Гурвица переходит в пессимистический критерий Вальда, а при a =1 – в критерий

максимального оптимизма.