End while

if Обмен = 1 then

y = y + s2

Else

x = x + s1

End if

 =  + 2*y

Next i

Finish

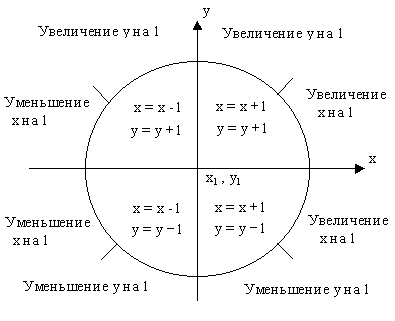
Рис.4.1. Разбор случаев для обобщенного алгоритма Брезенхема.

Пример 4.1. обобщенный алгоритм Брезенхема.

Для иллюсрации рассмотрим отрезок из точки (0,0) в точку (-8, -4).

начальные установки

x = 0

y = 0

x = 8

y = 4

s1 = -1

s2 = -1

Обмен = 0

е = 0

результаты работы пошагового цикла

i	Plot	е	x	y
	(0,0)
		-16		-1
		-8	-1	-1
	(-1,-1)
			-2	-1
	(-2,-1)
		-16	-2	-2
		-8	-3	-2
	(-3,2)
			-4	-2
	(-4,2)
		-16	-4	-3
		-8	-5	-3
	(-5,-3)
			-6	-3
	(-6,-3)
		-16	-6	-4
		-8	-7	-4
	(-7,-4)
			-8	-4

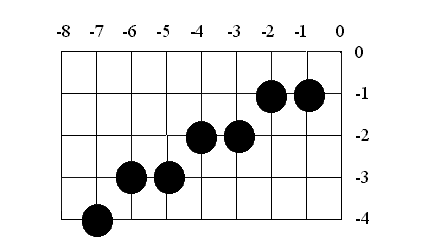
Рис.4.2. Результат работы обобщенного алгоритма Брезенхема в третьем квадранте.

На рис.4.2 продемонстрирован результат. Сравнение с рис. 2.2 показывает, что результаты работы двух алгоритмов отличаются.

В следующем разделе рассматривается алгоритм Брезенхема для генерации окружности.