2015-06-05
495
Теоретические (без учета потерь) значения основных параметров - давления и подачи вихревого насоса - могут быть получены из уравнения количества движения.
Пусть q - расход через межлопаточные каналы на единице длины отвода, м3 /(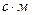
); с2u - среднее значение тангенциальной составляющей абсолютной скорости на выходе из межлопаточных каналов в отвод, м/с; c0 – средняя скорость потока в отводе, м/с.
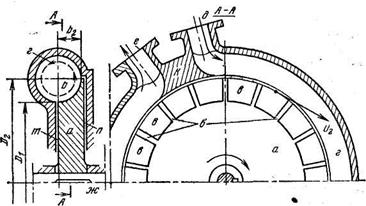
Рис. 9.1. Конструктивная схема вихревого насоса:
а - рабочее колесо; б - лопасти рабочего колеса; в - межлопастные каналы; ……………………….. г - отвод; д - всасывающий патрубок; ж - вал рабочего колеса; ……………………………………………….. к - разделитель потока
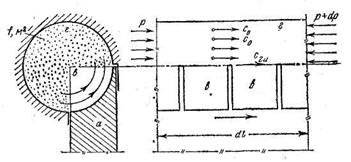
Рис. 9.2 К расчёту давления, развиваемого вихревым насосом
Если полагать приближенно ось отвода прямолинейной, то по схеме на рис. 9.2 уравнение количества движения для потока, выходящего из колеса в отвод,
,
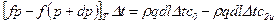Следовательно,
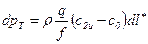. (9.1)
Из (9.1) видно, что давление в отводе нарастает в направлении движения пропорционально длине отвода.
Интегрирование (9.1) даёт теоретическое повышение давления на длине l отвода
.
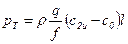Теоретическое повышение напора на длине l отвода
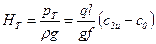. (9.2)
Расход в сечении отвода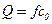 
, поэтому (9.2) приводит к следующему уравнению теоретической характеристики вихревого насоса:
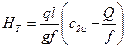. (9.3)
Вследствие постоянства q и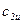 
по длине отвода уравнение (9.3) графически изображается прямой линией (рис. 9.3).
________________
В основу вывода формулы положена предельно упрощённая модель течения. Действительная картина течения и количественные зависимости чрезвычайно сложны.
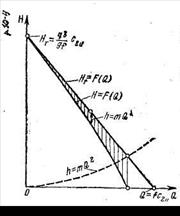
Рис. 9.3. Характеристики теоретического и действительного напоров вихревого насоса [к уравнению (9.3)]
Потери напора в проточной полости насоса пропорциональны квадрату подачи, поэтому, построив на графике на рис. 9.3 характеристики потерь напора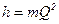 
, вычитанием ординат получаем характеристику действительного напора 
.
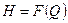Теоретическая мощность вихревого насоса
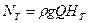
или, учитывая (9.3),
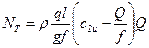. (9.4)
Это уравнение графически изображается квадратичной параболой с осью, параллельной оси ординат. Очевидно, что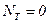 
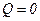при 
и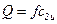 
(рис..9.4).
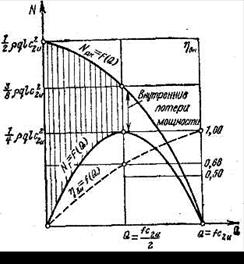
Рис. 9.4. Характеристика мощности и КПД вихревого насоса
Максимум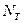 
находится дифференцированием 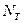по Q:
.
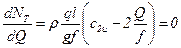Отсюда получим значение Q, при котором достигается (NТ)макс,
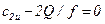, или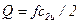 
.
Максимальное значение 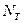по уравнению (9.4)
,
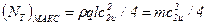где m – масса жидкости, проходящей в 1 с через межлопаточные каналы рабочего колеса.
Характеристика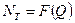 
показана на рис. 9.4.
Рабочее колесо вихревого насоса увеличивает тангенциальную составляющую скорости жидкости, проходящей через него, от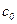 
до 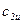; составляющая скорости вихревого течения в отводе и рабочем колесе по условию неразрывности сохраняется постоянной. Поэтому мощность, затрачиваемую рабочим колесом вихревого насоса, можно вычислить как разность секундных кинетических энергий потока на выходе и входе:
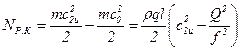. (9.5)
Значения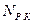 
для характерных подач, использованных при построении графика 
,
; 
;
; 
; 
; 
.
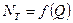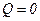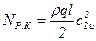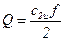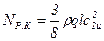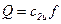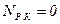По этим данным построен график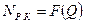 
(рис. 9.4).
Ввиду того что 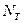- полезная теоретическая мощность, а 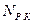- теоретическая мощность, затрачиваемая колесом, внутренний КПД вихревого насоса вычисляется как отношение 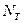к 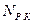, определяемое по (9.4) и (9.5),
.
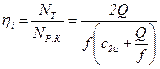Окончательное выражение для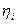 
получается подстановкой в последнее равенство :
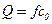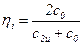. (9.6)
Величины 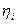для некоторых значений Q:
; 
; 
;
; 
; 
;
; 
; 
.
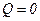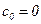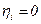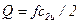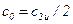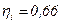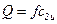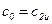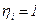Характеристика внутреннего КПД показана на рис. 9.4 штриховой линией.
Внутренние потери энергии, обусловленные передачей энергии от рабочего колеса потоку жидкости в отводе, представляются отрезками ординат между кривым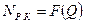и и .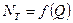
Из изложенного следует, что при постоянной частоте вращения рабочего колеса внутренние потери энергии в вихревом насосе тем больше, чем меньше подача. Следовательно, эксплуатация вихревого насоса в режиме значительного дросселирования нежелательна.
