Томас Мальтус (1766-1834) выдвинул свою известную теорию о росте народонаселения в геометрической прогрессии. На современном математическом языке эта зависимость отражает экспоненциальный рост численности организмов и описывается уравнением:
Nt = N0 ert,
где: Nt – численность популяции в момент времени t; N0 - численность популяции в начальный момент времени t0; r – показатель, характеризирующий темп размножения особей в данной популяции.
Экспоненциальный рост возможен только тогда, когда r имеет постоянное значение, так как скорость роста популяций пропорциональна самой численности.
Таким образом, экспоненциальный рост численности популяции – это рост численности ее особей в неизменяющихся условиях.
Условия, сохраняющиеся длительное время постоянными, невозможны в природе. В природе существует много ограничивающих факторов и поэтому экспоненциальный рост численности не наблюдается. Но есть примеры, когда при замедлении роста, т.е. при снижении r, экспоненциальный рост сохраняется, может он возникнуть и коротких отрезках жизни популяций.
Одним из первых, кто засомневался в полной адекватности модели Мальтуса, был бельгийский ученый Кетле (Quetelet). В 1835 году была опубликована его работа "Социальная физика или опыт исследования о развитии человеческих возможностей". В этой работе Кетле, как и позднее Чарльз Дарвин, обращает внимание на тот факт, что "склонность к размножению в геометрической прогрессии" присуща не только людям, но и всем живым существам, причем "у некоторых эта склонность гораздо развитее, чем у человека" (Ч. Дарвин пришел к этому заключению независимо от Кетле в 1838 году). Далее Кетле ставит под сомнение справедливость тезиса Мальтуса о неограниченном росте народонаселения. Он высказывает предположение о существовании некоторого состояния равновесия, как для численности населения, так и для численности биологических видов. По мере приближения к состоянию равновесия, согласно гипотезе Кетле, "замечается явное уменьшение склонности к размножению; народонаселение увеличивается, но с большим трудом, как будто ему приходится преодолевать сопротивление среды". Кетле предполагал, что «препятствия, задерживающие рост населения» увеличиваются пропорционально квадрату скорости прироста народонаселения. По просьбе Кетле, его друг, бельгийский математик Ферхюльст (Verhalst), провел более детальное исследование данного вопроса.
На основе анализа данных о динамике численности населения Бельгии и Франции, Ферхюльст отверг гипотезу Мальтуса о неограниченном экспоненциальном росте народонаселения и построил первую математическую модель, подтверждающую гипотезу Кетле о существовании состояния равновесия, к которому стремится численность населения. В отличие от Мальтуса, Ферхюльст предположил, что коэффициент r в (2.1) является не постоянной величиной, а линейно убывает с ростом величины N:
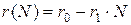 . . | (2.5) |
Подставляя (2.5) в (2.1), получим уравнение, которое Ферхюльст назвал логистичеким (от древнегреческого слова "логистика" — наука о вычислениях):
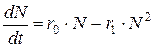 . . | (2.6) |
В отличие от идей Мальтуса, теория Ферхюльста была, к сожалению, на долгие годы забыта учеными. В двадцатые годы XX века, когда возникла необходимость математического моделирования динамики роста биологических популяций, экологи обратились к модели Мальтуса. Однако, эта модель хорошо описывала развитие популяций только на начальных этапах, когда популяция являлась немногочисленной и развивалась свободно, не испытывая недостатка в территории, пище или каких-либо других ограничений. В связи с этим возникла необходимость построения математической модели, описывающей развитие популяций, для которых наблюдается переход от роста с ускорением к замедлению роста и дальнейшая стабилизация численности. Тогда американскими экологами Пирлом (Pearl) и Ридом (Read) было заново открыто логистическое уравнение. Пирл записал его в несколько иной форме:
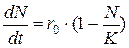 , , | (2.17) |
где 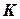 — максимальная численность популяции в условиях данной среды обитания. Эта величина получила название емкости среды обитания.
— максимальная численность популяции в условиях данной среды обитания. Эта величина получила название емкости среды обитания.
Величина 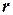 представляет собой относительную скорость прироста популяции при ее свободном развитии. Эта величина получила название биотического потенциала популяции. Уравнение (2.17) называют уравнением Ферхюльста-Пирла.
представляет собой относительную скорость прироста популяции при ее свободном развитии. Эта величина получила название биотического потенциала популяции. Уравнение (2.17) называют уравнением Ферхюльста-Пирла.
В случае, когда динамика популяции описывается уравнением Мальтуса, биотический потенциал 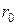 совпадает с величиной относительного прироста. Для логистической популяции относительный прирост является линейно убывающей функцией численности:
совпадает с величиной относительного прироста. Для логистической популяции относительный прирост является линейно убывающей функцией численности:
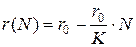 ,
,
что, как отмечалось выше, является исходной предпосылкой модели Ферхюльста. В результате решения уравнения логистической модели получим зависимость:
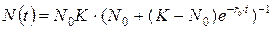
Величину относительного прироста численности можно рассматривать как разность коэффициентов рождаемости 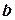 и смертности
и смертности 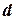 :
:
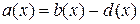 . . | (2.18) |
Линейное убывание относительного прироста численности соответствует линейному изменению коэффициентов рождаемости и смертности, при которых с увеличением численности коэффициент рождаемости убывает, а коэффициент смертности возрастает. Возможны также случаи, когда оба коэффициента убывают, но рождаемость падает быстрее, чем смертность, либо оба коэффициента увеличиваются, но смертность возрастает быстрее, чем рождаемость.
Наиболее распространенной в природе формой влияния численности популяции на изменение относительного прироста является монотонное увеличение смертности при монотонности падения рождаемости.
Мы рассмотрели наиболее простые модели динамики популяций на уровне так называемого полного внутрипопуляционного агрегирования, когда не учитываются внутренний состав и структура популяций. Кроме того, мы предполагали, что рассматриваемые популяции являются изолированными, то есть считали, что характеристики рассматриваемой популяции, в частности скорость ее роста, не зависят от изменений численности других популяций. В природе, как известно, полностью изолированных популяций не существует. Однако на начальных этапах развития популяций в ряде случаев можно пренебречь влиянием на их развитие других популяций, и тогда динамика исследуемых популяций, по крайней мере, качественно описывается рассмотренными выше моделями.
Чтобы иметь полную картину динамики численности популяции, а также рассчитать скорость ее роста, необходимо знать величину так называемой чистой скорости воспроизводства (R0), которая показывает, во сколько раз увеличивается численность популяции за одно поколение, во время его жизни Т.
R0 = NT/N0,
Где NT – численность нового поколения; N0 – численность особей предшествующего поколения. Если R0 = 1, то популяция стационарная, численность ее сохраняется постоянной.
Скорость роста популяции обратно пропорциональна длительности жизни поколения
r = ln R0/ Т,
отсюда ясно, что чем раньше происходит размножение организмов, тем больше скорость роста популяции. Это в равной степени относится и к популяции человека, отсюда – важность значения этой закономерности в демографической политике любого государства.
Воздействие экологических факторов на скорость роста популяций может довести численность популяций до стабильной (r = 0), либо уменшить ее, т.е. экспоненциальный рост замедлится или остановится полностью и экспоненциальная кривая выполаживается, превращаясь в так называемою S – образную кривую.
В природе так и происходит: экспоненциальный рост наблюдается, какое то время, после чего ограничивающие факторы его стабилизируют, и дальнейшее развитие популяции идет по логистической модели, что и описывается S – образной, или логистической кривой роста популяции.
Величину К называют емкостью среды в отношении особей данной популяции. Здесь речь идет о биологической емкости среды – степени способности природного или природно-антропогенного окружения обеспечивать нормальную жизнедеятельность (дыхание, питание, размножение и т.п.) определенному числу организмов и их сообществ без заметного нарушения самого окружения (Реймерс 1990).
Однако плато на S – кривой далеко не всегда бывает гладким, потому, что колебания численности происходит постоянно, что отражается в виде колебаний асимптоты К, эти колебания называются флуктуациями численности, которые могут быть сезонными и годовыми. Первые, обусловлены абиотическими факторами, вторые плюс к тому, еще и внутренними биотическими.
 2015-06-05
2015-06-05 1201
1201
