Пружинный маятник состоит из тела массы m и легкой пружины с коэффициентом жесткости k. В общем случае движение пружинного маятника в поле силы тяжести довольно сложно и описывается большим числом степеней свободы. Практический интерес, однако, представляют колебания с одной степенью свободы, когда движение маятника происходит вдоль вертикальной оси. Для того, чтобы маятник совершал только вертикальные колебания достаточно оттянуть тело строго вниз на небольшую величину. Для полного описания колебаний в этом случае необходимо знать поведение только одной переменной, например, вертикальной координаты центра масс тела маятника. На тело, подвешенное на пружине в поле силы тяжести действуют две силы (без учета сил трения) сила тяготения и упругая сила. Начало координат выберем таким образом, чтобы при х=О масса m находилась в равновесии. При этом сила тяжести mg будет скомпенсирована некоторым начальным растяжением пружины и в дальнейшем рассмотрении участвовать не будет.
При отклонении тела от точки равновесия будет возникать возвращающая сила F(х). Рассмотрим малые колония пружинного маятника. Колебания пружинного маятника называют малыми, если сила, возникающая при смещении грузика от положения равновесия, пропорциональна его смешению и направлена в сторону положения равновесия. Для пружинного маятника условия малости колебаний удовлетворяются при смещениях, создающих возвращающую силу у пружины в пределах применимости закона Гука.
Уравнение движения пружинного маятника при этом имеет вид
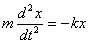 (1)
(1)
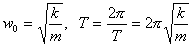 (2)
(2)
В реальных осцилляторах, за счет сил трения, происходит рассеяние (диссипация) запасенной энергии, в результате чего свободные колебания со временем затухают. При движения тела пружинного маятника в вязкой среде, с небольшими скоростями сила трения пропорциональна скорости. При учет диссипации энергии уравнение колебаний пружинного маятника имеет вид линейного дифференциального уравнения второй степени
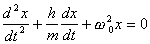 (3)
(3)
Решение этого уравнения имеет вид затухающих колебаний
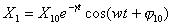 (4)
(4)
где X10, 10 — начальные амплитуда и фаза колебаний, w — частота затухающих колебаний, — декремент затухания. Действительно, подставим (4) в (3) получим
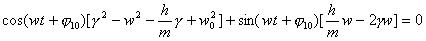 (5)
(5)
Отсюда следует, что
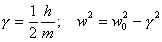 (6)
(6)
Используя полученный результат уравнение колебаний удобно записать в виде:
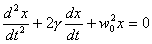 (7)
(7)
Для малых декрементов затухания колебания близки к гармоническим, при больших затухание происходит за 1—2 периода. В том случае, когда w0 значение частоты w становится мнимым и гармонические колебания не реализуются, происходит апериодический процесс—тело маятника после начального отклонения плавно возвращается в положение равновесия. Величина 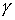 получила название декремента затухания. При этом величина
получила название декремента затухания. При этом величина 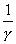 равна времени, за которое амплитуда колебаний затухает в е раз. Затухание колебаний за период
равна времени, за которое амплитуда колебаний затухает в е раз. Затухание колебаний за период
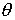 =
= 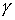 Т носит название логарифмического декремента затухания, его можно определить из соотношения
Т носит название логарифмического декремента затухания, его можно определить из соотношения
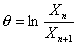 (8)
(8)
где 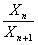 — отношение амплитуд двух последовательных колебаний.
— отношение амплитуд двух последовательных колебаний.
Упражнение 1. Определение коэффициента жесткости пружины при статической нагрузке.
1. Последовательно нагружая пружину 1 грузами массой 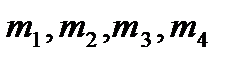 , измерил удлинение
, измерил удлинение 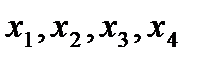 , вызванное каждыми из этих грузов, выполнил то же самое для пружины 2
, вызванное каждыми из этих грузов, выполнил то же самое для пружины 2
Пружина 1: Пружина 2:
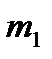 =200 г;
=200 г; 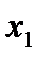 =21 мм;
=21 мм; 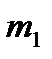 =200 г;
=200 г; 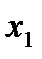 =23 мм;
=23 мм;
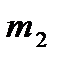 =300 г;
=300 г; 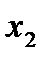 =41 мм;
=41 мм; 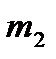 =300 г;
=300 г; 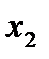 =29 мм;
=29 мм;
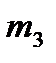 =400 г;
=400 г; 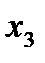 =67 мм;
=67 мм; 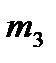 =400 г;
=400 г; 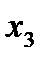 =42 мм;
=42 мм;
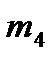 =500 г;
=500 г; 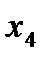 =90 мм;
=90 мм; 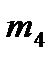 =500 г;
=500 г; 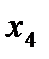 =55 мм;
=55 мм;
2. По формуле 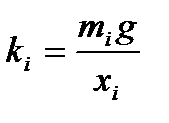 рассчитал коэффициент жесткости для первой пружины, аналогично рассчитал коэффициент жесткости для второй пружины.
рассчитал коэффициент жесткости для первой пружины, аналогично рассчитал коэффициент жесткости для второй пружины.
Пружина 1 Пружина 2
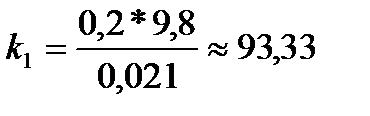
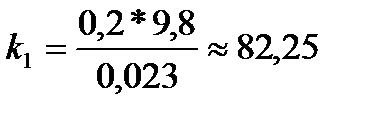
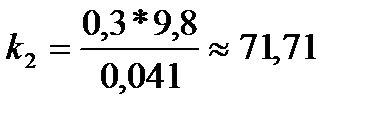
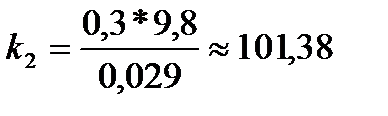
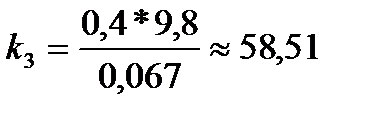
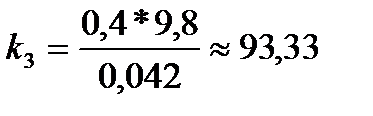
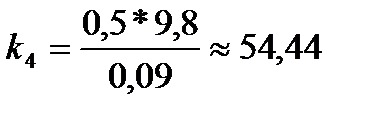

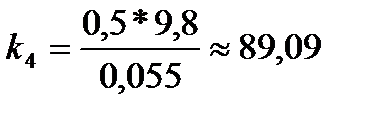
3. Нашел среднее значение 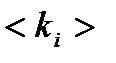 и погрешность в определении
и погрешность в определении 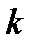 по формуле:
по формуле:
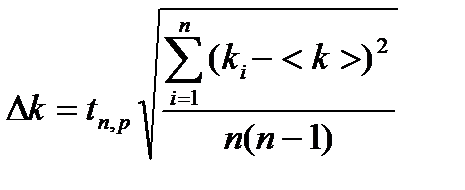 , где n – число измерений. Проделал то же самое для пружины 2.
, где n – число измерений. Проделал то же самое для пружины 2.
Пружина 1 Пружина 2
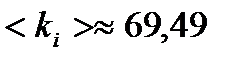
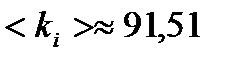
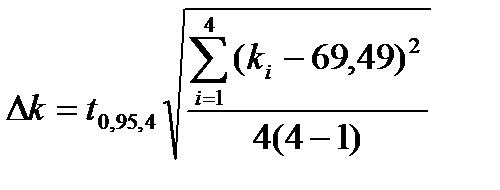
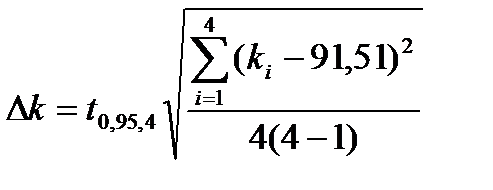
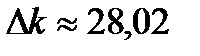
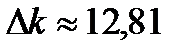
Упражнение 2. Определение логарифмического декремента затухания.
1. К пружине 1 подвесил груз массой m=500 г. Отвел груз от положения равновесия на 20 мм. Возбудил колебания груза на пружине. Измерил число колебаний, за которое амплитуда колебаний изменится с 20 до 15 мм. Опыт повторил 5 раз. Нашел логарифмический декремент затухания:
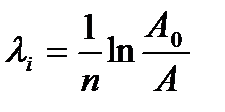 , где n – число колебаний;
, где n – число колебаний; 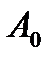 - начальная амплитуда;
- начальная амплитуда; 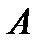 - амплитуда
- амплитуда  -го колебания.
-го колебания.
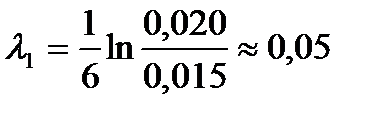 ;
; 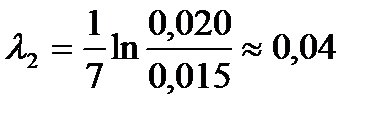 ;
; 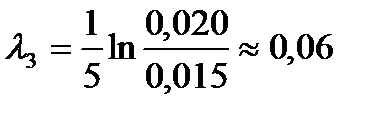 ;
; 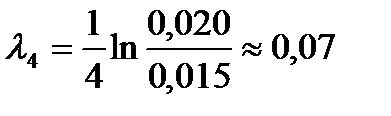 ;
; 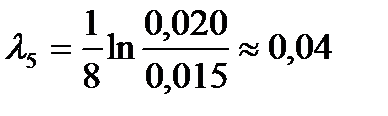 ;
;
2. Нашел 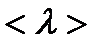 и
и 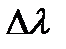 :
:
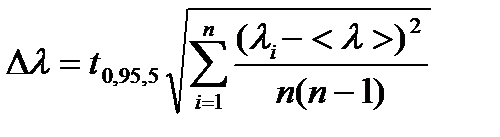 ;
; 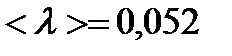 ;
; 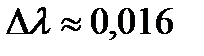 .
.
Закрепил на пружине демпфер. Определил, как указано выше, логарифмический декремент затухания. Сравнил логарифмический декремент затухания при наличии демпфера и без него.
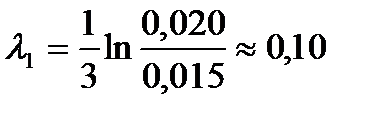 ;
; 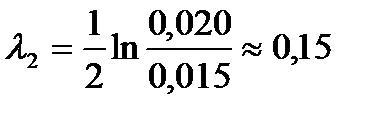 ;
; 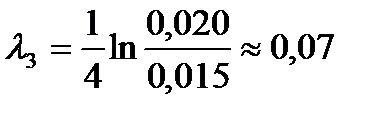 ;
;
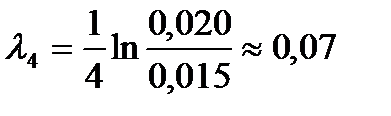 ;
; 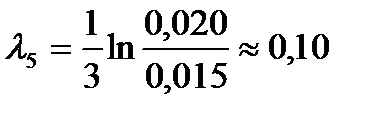 ;
; 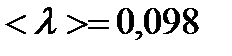 ;
; 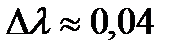 ;
;
Упражнение 3. Определение коэффициента жесткости при динамическом нагружении.
1. Выбрал пружину 1, исследованную статическим методом. К пружине подвесил груз массой 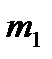 и возбудил колебания. Используя секундомер, измерил 5 раз время 10 полных колебаний (
и возбудил колебания. Используя секундомер, измерил 5 раз время 10 полных колебаний (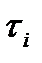 ) и вычислил период по формуле:
) и вычислил период по формуле:
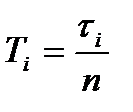 , где
, где 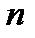 =10.
=10.
Нашел 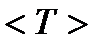 .
.
2. Проделал с грузами 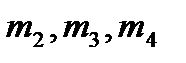 то же самое.
то же самое. 
Масса 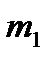 Масса
Масса  Масса
Масса 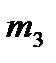 Масса
Масса 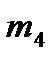
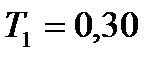
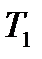 =0,46
=0,46 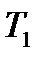 =0,46
=0,46 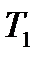 =0,46
=0,46
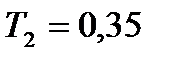
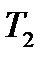 =0,46
=0,46 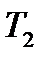 =0,46
=0,46 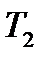 =0,40
=0,40
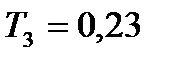
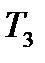 =0,35
=0,35 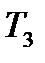 =0,52
=0,52 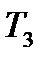 =0,46
=0,46
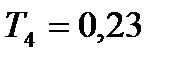
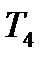 =0,35
=0,35 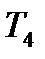 =0,40
=0,40 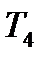 =0,35
=0,35
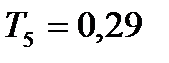
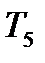 =0,40
=0,40 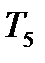 =0,46
=0,46 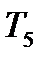 =0,52
=0,52
< T >=0,28 < T >=0,40 < T >=0,46 < T >=0,91
3. Используя результаты измерений, построил график зависимости квадрата периода колебаний 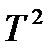 от массы m.
от массы m.
4. Нашел из графика 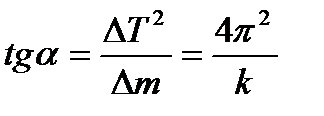 .
. 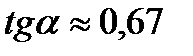 .
.
5.По формуле 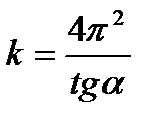 вычислил коэффициент жесткости.
вычислил коэффициент жесткости. 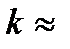 59
59
6. Сравнил значения жесткости пружины, полученные статическим методом и из углового коэффициента графика. Результаты отличаются друг от друга на 10,49. Эта разница объясняется погрешностью измерительных приборов метода измерения.
Вывод: я научился определять коэффициент жесткости пружины при статическом нагружении, логарифмический декремент затухания, коэффициент жесткости при динамическом нагружении.
 2015-06-05
2015-06-05 2485
2485






