Классический метод проверки гипотез

В соответствии с поставленной задачей и на основании выборочных данных формулируется (выдвигается) гипотеза 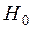, которая называется основной или нулевой. Одновременно с выдвинутой гипотезой 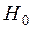, рассматривается противоположная ей гипотеза 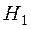, которая называется конкурирующей или альтернативной.

Для проверки нулевой гипотезы вводят специально подобранную случайную величину 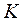, распределение которой известно и называют ее критерием.

Поскольку гипотеза 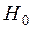для генеральной совокупности принимается по выборочным данным, то она может быть ошибочной. При этом возможны ошибки двух родов.

Ошибка первого рода состоит в том, что отвергается гипотеза 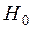, когда она на самом деле верна.

Ошибка второго рода состоит в том, что отвергается альтернативная гипотеза 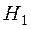, когда она на самом деле верна.

1) Для определения вероятности ошибки первого рода вводится параметр :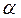

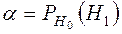
- вероятность того, что будет принята гипотеза 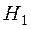, при условии, что 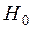верна.

Величину 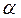называют уровнем значимости. Обычно 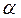выбирают в пределах .

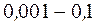2) Вероятность ошибки второго рода определяется параметром :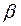

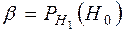
- вероятность того, что будет принята гипотеза 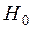, при условии, что 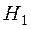верна.

Величину 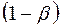, то есть недопустимость ошибки второго рода (отвергнуть неверную и принять верную гипотезу 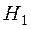) называют мощностью критерия.