В современных учебниках, пособиях и различного рода задачниках, к сожалению, уделяется мало внимания психологическим факторам, влияющим на успешность обучения математике. А именно, воспитание у учащихся уверенности в своих силах, развитие умения пользоваться прошлым опытом.
Берутся два общеизвестных утверждения, которые являются базовыми. На основе этих утверждений выстраиваются две «цепочки» задач по нарастающему уровню сложности. Решения задач в этих «цепочках» основаны на базовых утверждениях и на решении предыдущих задач.
Утверждение 1. Два треугольника являются равновеликими, если равны их высоты и основания.
Задача 1. Докажите, что диагональ параллелограмма делит его на два равновеликих треугольника.
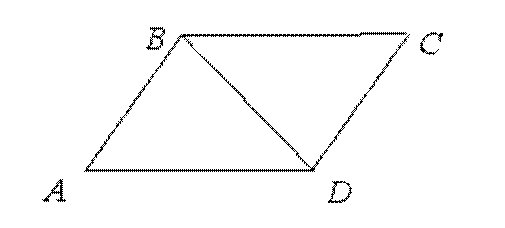
Решение. Высоты треугольников ABD и BCD равны. AD = BC (по свойству параллелограмма). Тогда в силу утверждения 1 S ▲ ABD = S ▲ BCD
Задача 2. На стороне CD параллелограмма ABCD взята произвольная точка Е. Зная, что S▲ABE = S, найдите площадь параллелограмма ABCD.
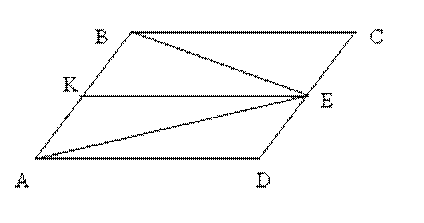
Решение. Проведем дополнительное построение: КЕ ║ AD. Тогда из задачи 1 следует, что S ▲ KBE = S ▲ CBE , а S ▲ AK E = S ▲ADE. Отсюда S ABCD = 2 S.
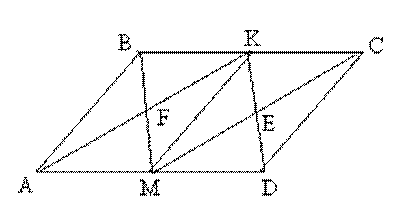
Задача 3. В параллелограмме ABCD на сторонах AB и CD взяты произвольные точки M и N. Докажите, что площадь четырехугольника KMEN равна площади четырех образовавшихся треугольников.
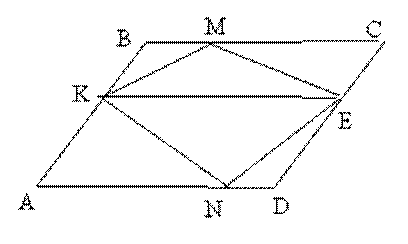
Решение. Проведем отрезок КЕ. Тогда в силу задачи 2 S ▲ KME = S ▲ KMB + S ▲ MEC , а S▲KNE = S▲AKN + S▲EDN
Отсюда S▲KMEN = S▲KMB + S▲MEC + S▲KNE + S▲EDN
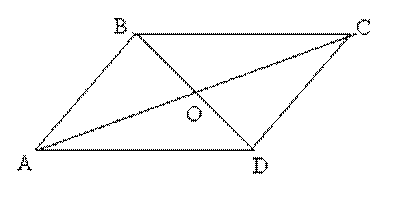
Задача 4. Внутри параллелограмма ABCD взята произвольная точка О. Зная площадь трех треугольников с вершиной в точке О, найдите площадь четвертого треугольника.
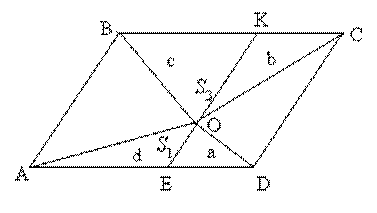
Решение. Пусть S▲ADO = S 1, S▲ABO = S 2,
S▲BOC = S 3. Произведем дополнительное построение: КЕ ║ АВ.
Введем следующие обозначения:
S▲EOD = a, S▲KCO = b, S▲BKO = c, S▲AEO = d.
Тогда S 2 = с + d, S▲DOC = a + b, S 1 + S 3 = a + b + c + d.
Отсюда S▲DCO = S 1 + S 3 - S 2
Задача 5. Каждая диагональ четырехугольника делит его на треугольники одинаковой площади. Докажите, что это параллелограмм.
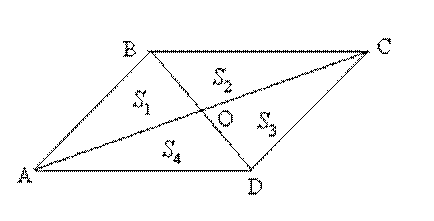
Решение. Из условия следует, что верны равенства: S 1 + S 2 = S 3 + S 4 и S 1 + S 4 = S 3 + S 2. Откуда получим, что S 1 = S 3, а S 2 = S 4. Отметим, что S2:S1= AO:ОС, S4:S3=AO:OC. Кроме этого, соответствующие высоты треугольников BOC, COD и AOB, AOD равны, соответственно, площади относятся как длины оснований. Из того, что S 1 = S 3 и S 2 = S 4. следует, что AO:OC =AO: OC. Следовательно, AO = OC. Аналогично можно доказать, что BO = OD. Можно сделать вывод, что диагонали четырехугольника точкой пересечения делятся пополам, а это значит, что ABCD - параллелограмм.
Утверждение 2. Медиана треугольника делит его на два равновеликих треугольника.
Задача 6. В параллелограмме ABCD точка К – середина АВ, а L – середина ВС. Зная, что SKBLD = S, найдите SABCD.
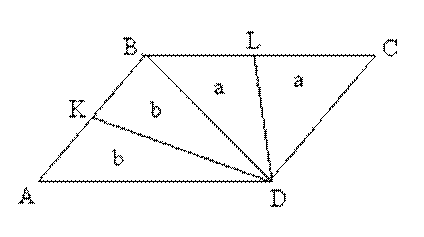
Решение. Проведем диагональ ВD. Тогда, исходя из утверждения 2, получим, что SABCD = 2S.
Задача 7. В четырехугольнике ABCD точка Е, середина АВ, соединена с вершиной D, а точка F, середина CD, - с вершиной В. Докажите, что S ABCD = 2 SEBFD
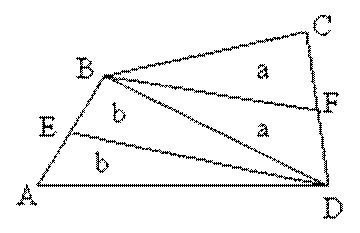
Решение. Проведя диагональ ВD и рассуждая аналогично задаче 6, получим, что S ABCD = 2 SEBFD
Задача 8. В произвольном четырехугольнике проведены отрезки, соединяющие середины сторон этого многоугольника. Зная площади
трех из полученных четырехугольников, найдите площадь четвертого.
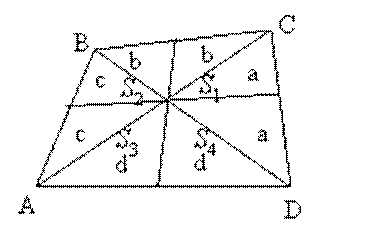
Решение. В силу утверждения 2 и обозначений, использованных для элементов чертежа, получим S 1 = a + b, S 2 = b + c, S 3 = c + d, S 4 = a + d. Тогда, зная S 1, S 2, S 3, S 4 получим, что S 4 = S 1 + S 3 - S 2.
Задача 9. Докажите, что диагонали параллелограмма делят его на четыре равновеликих треугольника.
Решение. В силу задачи 1 и утверждения 2 будем иметь
S▲AOB = S▲BOC = S▲COD =S▲DOA
Задача 10. Середины двух параллельных сторон параллелограмма соединены с противолежащими вершинами. Какая часть площади параллелограмма ограничена проведенными отрезками?
Решение. Проведем отрезок МК. Тогда в силу задачи 9 SMFKE = 1/4SABCD.
Задача 11. Дан выпуклый четырехугольник ABCD. Середины сторон АВ и CD обозначены соответственно через К и М, точку пересечения отрезков ВМ и СК – через Р, точку пересечения отрезков АМ и DК – через О. Докажите, S MOKP = S▲BPC + S▲AOD
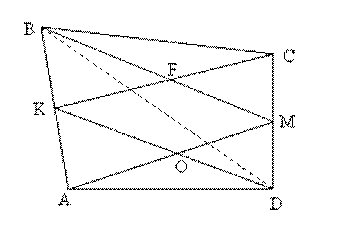
Решение. Проведем диагональ ВD. Так как DК и ВМ медианы вновь полученных треугольников, то SAKD=1/2SABD, SBMC=1/2SBCD. Отсюда S▲AKD + S▲BMC = 1/2SАВСD (1) Проведя диагональ АС и учитывая, что АМ и СК медианы уже вновь полученных треугольников, получим SKBC=1/2SABC, SAMD=1/2SACD.
Тогда S▲KBC + S▲AMD = 1/2SABCD (2).
Из равенств (1) и (2) следует, что S▲AKD + S▲BMC + S▲KBC + S▲AMD = SABCD.
В этой сумме дважды учтены площади треугольников ВРС и АОD, но не учтена площадь четырехугольника МОКР. Поэтому SMOKP = S▲BPC + S▲AOD.
Задача 12. На продолжениях сторон выпуклого четырехугольника АВСD отложены отрезки BB 1 = AB, CC 1 = BC, DD 1 = CD и AA 1 = AD. Докажите, что площадь четырехугольника А 1 В 1 С 1 D 1 в 5 раз больше площади четырехугольника АВСD.
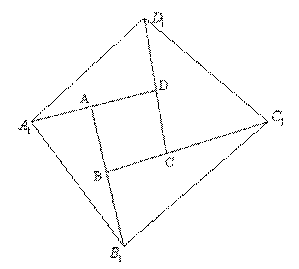
Решение. Медиана делит площадь треугольника пополам, поэтому площади треугольников ABC, BB 1 C и CC 1 B 1 равны между собой. Площадь треугольника ACD равна площади треугольника ADD 1, площадь треугольника ADD 1 равна площади треугольника AA 1 D 1 и т. д. Тогда S▲ BB1C1 = 2 S▲ABC, S▲ CC1D1 = 2 S▲BCD, S▲ AA1B1 = 2 S▲DBA, S▲ DD1A1 = 2 S▲CAD. Суммируя эти равенства, получим S▲ BB1C1 + S▲ CC1D1 + S▲ AA1B1 + S▲ DD1A1.Обозначим площадь четырехугольника АВСD через S, тогда площадь четырех построенных треугольников равна 4 S, а площадь четырехугольника А 1 В 1 С 1 D 1 равна 5 S.
Задача 13. Вершина А квадрата АВСD соединена с точкой О – серединой ВС, вершина В – с точкой Е – серединой СD, вершина С – с точкой N – серединой АD, а вершина D – с точкой К – серединой АВ. Точки пересечения проведенных прямых L, M, R, и Р служат вершинами четырехугольника LMRP.
Докажите, что SLMRP=51SABCD.
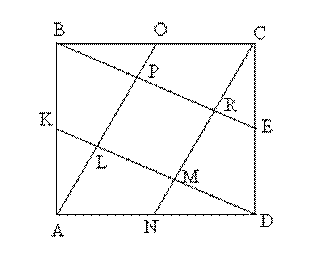
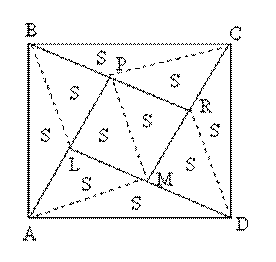
Решение. ВКDE – параллелограмм, так как ВК = DE и ВК? DE, поэтому ВЕ? К D. АОСN – параллелограмм, так как АN = ОС и АN? ОС, поэтому ОА? СN. Учитывая, что О, Е, N, и К – середины сторон, из теоремы Фалеса следует, что АL = LP, BP = PR, CR = RM и DM = ML. Для большей наглядности дальнейшего хода решения задачи, представим чертеж в другом виде. Дальнейший ход решения совпадает с решением задачи 12.
Продолжим «цепочку» задач, исходной фигурой в которых будет выступать уже треугольник.
Задача 14. На продолжении стороны АВ треугольника АВС взята точка К так, что АВ = ВК. Точка L – середина ВС. Зная, что S▲BKL = S, найдите S▲ABC.
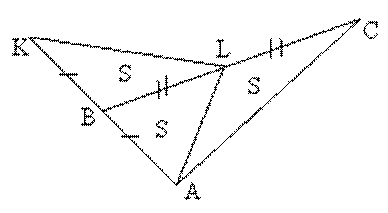
Решение. Сделаем дополнительное построение – проведем отрезок AL. В силу утверждения 2 и использованных на чертежах обозначений S▲ABC = 2 S.
Задача 15. На продолжении сторон треугольника АВС построены отрезки AA 1 = AC, BB 1 = AB и CC 1 = BC. Докажите, что S▲ A1B1C1 = 7 S▲ABC.
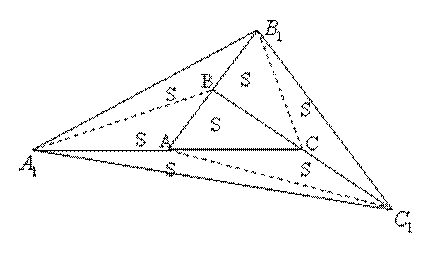
Решение. Произведя дополнительные построения, приняв во внимание обозначения на чертеже и опираясь на утверждение 2, видим, что решение следует непосредственно из чертежа.
Задача 16. На продолжении стороны треугольника АВС взята точка D так, что АС = СD. Пусть М – середина стороны АВ, а К – точка пересечения отрезков ВС и МD. Докажите, что площадь треугольника ВКD равна площади четырехугольника АМКС.
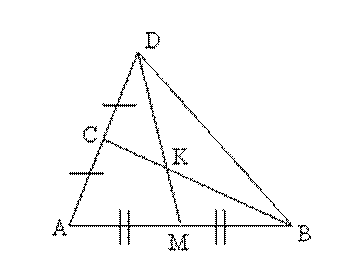
Решение. В треугольнике АВD DМ и ВС – медианы. Поэтому S ▲AMD =S▲BMD и S ▲ACB = S▲CDB. Эти равенства можно записать так: SAMKC + S ▲CKD = S▲MDK + S▲BKD, SAMKC + S ▲MBK = S▲CKD + S▲BKD
Сложив эти равенства и упростив выражение, получим SAMCK = S▲BKD.
Опорные задачи, решаемые методом площадей
Метод площадей имеет много разновидностей. Его применяют, например, при замене отношения отрезков, расположенных на одной прямой, отношением площадей треугольников с общей вершиной, основаниями которых являются рассматриваемые отрезки.
При решении задач методом площадей часто применяют основные формулы, выражающие площадь треугольника.
Обозначим, через А, В и С величины соответствующих углов треугольника АВС, а через а, b и с, как обычно, длины противолежащих им сторон, 2р – периметр треугольника, r и R – соответственно радиус вписанной и описанной окружности.
В этих обозначениях для площади треугольника справедливы следующие формулы:
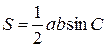 (2.1)
(2.1)
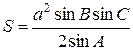 (2.2)
(2.2)
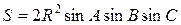 (2.3)
(2.3)
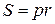 (3.4)
(3.4)
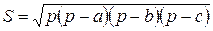 (2.5)
(2.5)
Формулы (1), (4) и (5) хорошо известны, формулы (2), (3) получаются из формулы (1), используя теорему синусов. Формула (4) справедлива для любого описанного многоугольника.
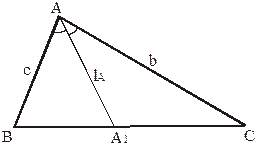
Используя формулу (1) для площади треугольника, можно доказать теорему о биссектрисе внутреннего угла треугольника.
Теорема. Если 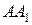 – биссектриса угла А треугольника АВС, то
– биссектриса угла А треугольника АВС, то 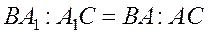 .
.
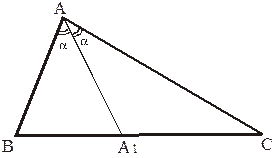 Доказательство. Пусть угол при вершине А в треугольнике АВС равен
Доказательство. Пусть угол при вершине А в треугольнике АВС равен 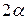 . Рассмотрим треугольники
. Рассмотрим треугольники 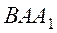 и
и 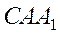 (рис. 10). Их площади относятся как отрезки
(рис. 10). Их площади относятся как отрезки 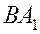 и
и 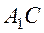 .
.
Используя формулу (2.1) имеем
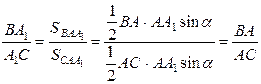 .
.
Рассмотрим опорные задачи, решаемые методом площадей.
Пример 1. Пусть две прямые пересекаются в точке А. В и В1 – любые две точки на одной прямой, а С и С1 – на другой. Докажите, что 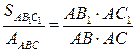 .
.
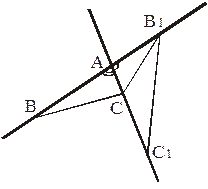 Решение. Углы при вершине А треугольников АВС и АВ1С1 либо равны, либо дополняют друг друга до 1800 (рис. 11), то есть в любом случае синусы этих углов равны. Используя формулу (2.1) для площади треугольника имеем
Решение. Углы при вершине А треугольников АВС и АВ1С1 либо равны, либо дополняют друг друга до 1800 (рис. 11), то есть в любом случае синусы этих углов равны. Используя формулу (2.1) для площади треугольника имеем 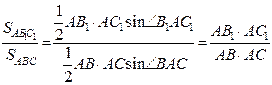 .
.
Пример 2. На сторонах АВ и АС треугольника АВС взяты точки В1 и С1 так, что 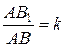 ,
, 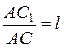 . Докажите, что
. Докажите, что 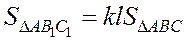 .
.
Решение следует непосредственно из предыдущего примера.
Пример 3. Докажите, что длину биссектрисы 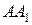 треугольника АВС можно вычислить по формуле
треугольника АВС можно вычислить по формуле 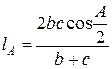 , где
, где 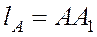 ,
, 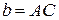 ,
, 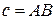 , А – угол ВАС.
, А – угол ВАС.
 Решение. Учитывая свойство 3 площади, имеем
Решение. Учитывая свойство 3 площади, имеем 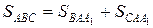 или
или 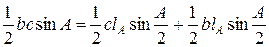 . Заменив в левой части равенства
. Заменив в левой части равенства 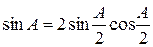 и сократив обе его части на
и сократив обе его части на 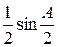 , получим
, получим 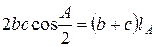 , откуда
, откуда 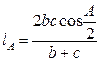 .
.
Рассмотрим еще одну полезную задачу.
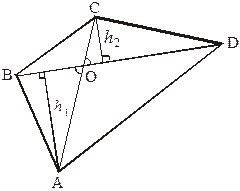 Пример 4. Пусть О – точка пересечения диагоналей четырехугольника ABCD. Тогда имеет место равенство
Пример 4. Пусть О – точка пересечения диагоналей четырехугольника ABCD. Тогда имеет место равенство 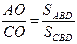 .
.
Решение. Пусть 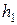 и
и 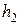 высоты треугольников ABD и CBD, проведенные к стороне BD (рис. 13). Очевидно, что
высоты треугольников ABD и CBD, проведенные к стороне BD (рис. 13). Очевидно, что 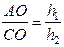 .
. 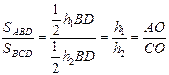 .
.
Используя результаты предыдущих задач, рассмотрим еще один важный пример, который в учебнике И.Ф. Шарыгина «Геометрия. 7-9 классы» назван типичной задачей.
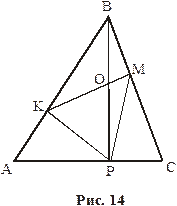 Пример 5. В треугольнике АВС на сторонах АВ, ВС и СА взяты соответственно точки К, М и Р так, что АК:КВ=2:3, ВМ:МС=3:4, СР:АР=4:5. В каком отношении отрезок ВР делится отрезком КМ?
Пример 5. В треугольнике АВС на сторонах АВ, ВС и СА взяты соответственно точки К, М и Р так, что АК:КВ=2:3, ВМ:МС=3:4, СР:АР=4:5. В каком отношении отрезок ВР делится отрезком КМ?
Решение. Пусть ВР и КМ пересекаются в точке О (рис. 14) и 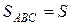 . Так как
. Так как 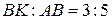 ,
, 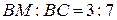 , то
, то 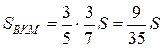 . Так как
. Так как 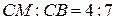 ,
, 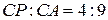 , то
, то 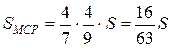 . Так как
. Так как 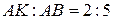 ,
, 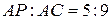 , то
, то 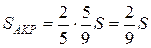 . Следовательно,
. Следовательно, 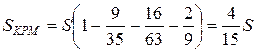 и
и 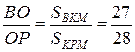 .
.
При решении задач методом площадей следует помнить, что
1)Диагонали трапеции делят ее на четыре треугольника. Треугольники, прилежащие к боковым сторонам, равновелики.
2) Диагонали выпуклого четырехугольника делят его на четыре треугольника. Произведение площадей треугольников прилегающих к противоположным сторонам равны.
 2015-06-05
2015-06-05 5396
5396
