Cпособы определения площадей в геодезии

Определение площадей земельных участков является одним из важнейших видов геодезических работ для целей земельного кадастра.

В зависимости от хозяйственной значимости земельных участков, наличия планово-топографического материала, топографических условий местности и требуемой точности применяют различные способы определения площадей.

1. Аналитический, когда площадь вычисляется по результатам измерений линий на местности, по результатам измерений линий и углов на местности или по их функциям (координатам вершин фигур).

2. Графический, когда площадь вычисляется по результатам измерений линий или координат на плане (карте). Графические способы. Участок на плане разбивают на простые геометрические фигуры (обычно – треугольники), элементы которых измеряют с помощью измерителя и поперечного масштаба, а площади вычисляют по известным формулам и суммируют.

3. Механический, когда площадь определяется по плану с помощью специальных приборов (планиметров) или приспособлений (палеток). Иногда эти способы применяют комбинированно, например, часть линейных величин для вычисления площади определяют по плану, а часть берут из результатов измерений на местности.

Площади можно также определить на ЭВМ по цифровой модели местности по специальной программе.

При аналитическом способе определения площадей применяются формулы геометрии, тригонометрии и аналитической геометрии. При определении площадей небольших участков (для учета площадей, занятых строениями, усадьбами, площадей вспашки, посева) участки разбиваются на простейшие геометрические фигуры, преимущественно треугольники, прямоугольники, реже трапеции. В этом случае площади участков определяются как суммы площадей отдельных фигур, вычисляемых по линейным элементам - высотам и основаниям.

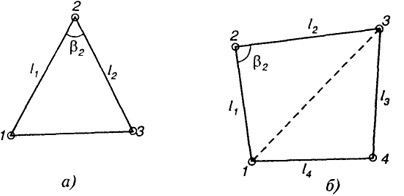
Рис. 23.1. Геометрические фигуры для определения площадей участков (а, б)

Если по границам участка выполнены геодезические измерения, то площадь всего участка или его части можно вычислить по формулам, приведенным применительно к следующим фигурам участков (рис. 23.1).

Треугольник (рис. 23.1, а). Площадь треугольника определяется по сторонам l ₁ и l ₂, углу β₂, заключенному между ними, по формуле

P = (l ₁· l ₂·sinβ₂). (23.1)

Четырехугольник (рис. 23.1, б). В зависимости от элементов, известных в четырехугольнике, могут быть использованы различные формулы для расчета, в связи с чем приведем пример, характеризующий это многообразие. Пусть в четырехугольнике измерены все стороны и один угол при вершине 2. В таком случае площадь треугольника 1 - 2 - 3 может быть вычислена по формуле (23.1). При этом полезно вычислить длину l _1-3, используя теорему косинусов

l _1-3 = √

+ l ² -2· l ₁· l ₂·cosβ.(23.2)

Площадь треугольника 1 - 3 - 4 может быть вычислена по формуле

P = √ S ·(S - l ₃)·(S - l ₄)·(S - l _1-3),(23.3)

где S - полупериметр, равный

S =

(l ₃ + l ₄ + l _1-3).

Общая площадь четырехугольника будет равна:

P =

·sinβ₂ + √ S ·(S - l ₃)·(S - l ₄)·(S - l _1-3).(23.4)