2015-06-04
2424
Как мы уже отмечали ( разд. 1), метрологическая(измерительная) информация формируется (вырабатывается) в процессе измерения некоторой (в частности – действительной) величины посредством измерительной аппаратуры (например, с помощью аналого-цифрового преобразователя аналоговых сигналов), а на результаты измерения оказывают случайные воздействия различные непреднамеренные помехи.
Если измерительный прибор предварительно откалиброван, то в процессе измерения не возникает систематических погрешностей, а точность результата измерения характеризуется известной дисперсией D п = σп2 случайных погрешностей измерений.
Как охарактеризовать количество измерительной информации, вырабатываемой в процессе измерения некоторой величины, например напряжения u 0 (в Вольтах), которая может принимать произвольное значение x = x 0 на множестве действительных чисел (– ∞ < x < ∞)?
К. Шеннон не проводил отдельного анализа этой ситуации, а постулировал ([46], с. 296):
«Энтропия дискретного множества вероятностей p 1, …, pn была определена как
|
|
|
H = –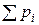 
log pi. (11.1)
Аналогичным образом определим энтропию непрерывного распределения с функцией плотности распределения p (x) как
H = –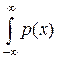 
log p (x) dx ». (11.2)
Н. Винер при введении «разумной меры количества информации» для «непрерывных сообщений» типа (11.1) ссылается на личное сообщение Дж. фон Неймана ([10], с. 121) и вводит её как H = +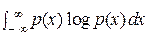 
.
При этом Н. Винер отмечает ([10], с. 122):
«Величина, которую мы здесь определяем как количество информации, противоположна по знаку величине, которую в аналогичных ситуациях обычно определяют как энтропию. Данное здесь определение не совпадает с определением Р. А. Фишера для статистических задач, хотя оно также является статистическим определением и может применяться в методах статистики вместо [выделено мною – Г. Х.] определения Фишера».
В дальнейшем в математической теории информации приняли определение (11.2) К. Шеннона. Однако формально-математическое обобщение выражения (11.1) на непрерывные распределения p α(x) случайной величины α приводят к следующему противоречию:
H (x) =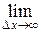 
{ 
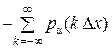Δ x log [ p α(k Δ x) Δ x ]} =
= – { 
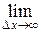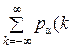Δ x) log [ p α(k Δ x)] Δ x } – 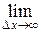[log Δ x 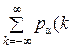Δ x) Δ x ],
или H (x) = –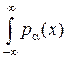 
log [ p α(x)] dx – 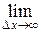[log Δ x ],
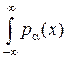или H (x) = – 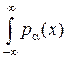log [ p α(x)] dx + ∞. (11.3)
Бесконечность в выражении (11.3) обычно («из практических соображений») отбрасывают, а интегралh (x) = –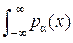 
log [ p α(x)] dx называют дифференциальной (относительной, сведённой) энтропией.
Например, при гауссовском распределении p α(x) погрешностей измерений
h (x) =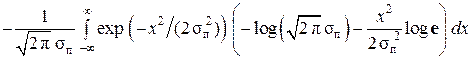 
,
или h (x) = lo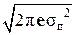g 
= log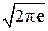 
+ log σп.
Поскольку величина (2 π e) играет большую роль в ПТИ, введём для неё специальное обозначение μ0 = 2 π e ≈ 17,1. Поэтому дифференциальную энтро-
|
|
|
пию h (x) гауссовского распределения p α(x) будем записывать в виде
h (x) = log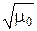 
+ log σп = 
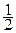log (μ 0 D п).
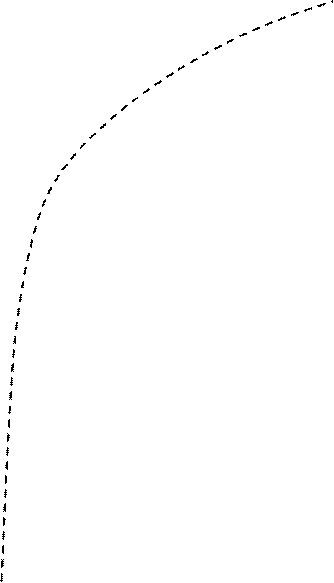
Зависимость h (x) от величины σп представлена на рис. 12. Там же приведена зависимость от σп информационной меры Неймана-Винера.
I
3 
2
1 σ n –2
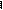
0,242 σ n
0 1 2 3
– 1
– 2
– 3 
Рис. 12. Зависимость количества информации I,
вырабатываемой при однократном измерении величины u 0,
от среднеквадратического значения погрешностей измерений σ n
Дифференциальная энтропия h (x) имеет следующие особенности.
а) Она может быть как положительной, так и отрицательной:
h (x) = 0 при σп = (2 π e) – 1/2 ≈ 0,242.
б ) Она растёт с увеличением дисперсии D п = σп2 погрешностей измерений (то есть чем точнее измерительный прибор, тем меньше информации получается в результате его использования). Правда, мера Неймана-Винера имеет «правильную зависимость»: она даёт уменьшение количества измерительной информации с увеличением дисперсии D п.
в) Она имеет «странную» размерность; например [log (Вольт)].
г) Она изменяется при формальном изменении масштаба по оси O x.
д) Она не обладает свойством аддитивности относительно дисперсии D п.
Действительно. Если в нашем распоряжении имеются результаты двух независимых измерений x 1 и x 2, обладающих дисперсиями погрешностей D 1 и D 2, то их совместная плотность вероятности есть: p (x 1, x 2) = p (x 1) p (x 2). Дифференциальная энтропия в этом случае формально определяется как
h (x) = –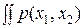 
log p (x 1, x 2) dx 1 dx 2 =
= – 
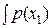log p (x 1) dx 1 – 
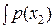log p (x 2) dx 2
и при гауссовских законах распределения p (x 1) и p (x 2) она равна:
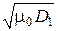h (x) = log 
+ log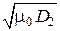 
, или h (x) = log μ 0 + log σ1 + log σ2.
Если рассуждать «негэнтропийно», то следует полагать, что до измерения (априори) мы имели некоторую большую неопределённость измеряемой величины x 0, характеризуемую дифференциальной энтропией h (x) = log σ0 + log ,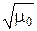
где величина σ0 определяется нашими предположениями относительно ожидаемого значения величины x 0.
Если мы провели измерение неизвестной нам величины x 0 и получили апостериорное значение x 1 со среднеквадратической погрешностью σ1, то, согласно негэнтропийной точки зрения, мы получили количество измерительной информации: I 1 = h (x 0) – h (x 1) = log σ0 – log σ1 = log (σ0 /σ1) > 0.
Если мы имеем результаты двух независимых измерений x 1 и x 2 величины x 0 со среднеквадратическими погрешностями измерений соответственно σ1 и σ2, то мы должны считать, что получили количество измерительной информации
I 1 + I 2 = log (σ0 /σ1) + log (σ0 /σ2) = log [σ02/(σ1 σ2)].
Суммарное количество информации (I Σ = I 1 + I 2) должно быть выражено через дифференциальную энтропию, то есть иметь вид I Σ = log (σ0 /σΣ). Однако из теоретической метрологии, как будет показано ниже, следует, что при оптимальном способе точечного оценивания величины x 0 по результатам двух независимых измерений x 1 и x 2 дисперсия оптимальной оценки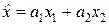 
будет минимально возможной и составлять величину D Σ = σΣ2 = 1/(σ1–2 + σ2–2).
Значит, при негэнтропийной трактовке процесса выработки измерительной (метрологической) информации имеем:
I Σ = log(σ0 /σΣ) =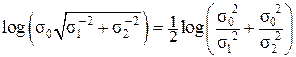 
,
или I Σ =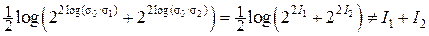 
.
Если же считать, что результат второго измерения x 2 является апостериорным по отношению к первому x 1, то при втором измерении мы получим количество информации I 21 = log (σ1 /σ2). При σ1 = σ2 ( равноточные измерения): I 21 = log (σ1 /σ1) = 0, а если σ2 > σ1, то I 21 = log (σ1 /σ2) < 0.
Это явно противоречит интуитивному понятию о количестве информации, получаемой в процессе измерений, то есть в процессе выработки измерительной (метрологической) информации.
Как видим, формально-математическое обобщение меры знаковой (семиотической, дискретной) информации на измерительную (метрологическую, «непрерывную») информацию приводит к нарушению основных постулатов теории информации.
|
|
|
Вернёмся к основным постулатам теории информации и попытаемся непротиворечивым образом ввести информационную меру для измерительной (метрологической) информации.
Пусть измеряется некоторая величина x 0, которая может принимать любые значения из множества действительных чисел (– ∞ < x < ∞). Откалиброванный измерительный прибор не имеет систематической погрешности измерений (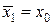
) и имеет дисперсию погрешностей измерений D 1 = σ12. Какое количество информации формирует (вырабатывает) этот измерительный прибор, если в результате одного измерения получено значение x = x 1?
Очевидно, что измеряемая величина x 0 с некоторой вероятностью P ≈ 1 лежит в пределах (x 1 – c σ1) < x 0 < (x 1 + c σ1), где c > 1 (интервальное оценивание: Ежи Нейман, 1937 г., или «остаточная неопределённость» результата измерения).
По аналогии со знаковой (семиотической) информацией (см. разд. 3) мы должны потребовать следующее.
а) Полученная в результате однократного измерения информация I (x 1) должна быть неотрицательной: I (x 1) ≥ 0.
б) Чем меньше дисперсия погрешностей D 1 измерительного прибора, тем точнее интервальная оценка (меньше «остаточная неопределённость») и тем больше информации мы получаем в результате однократного измерения x 1;
в) Если мы получили второе измерение x 2 другим прибором, характеризующимся большей дисперсией D 2 погрешностей (D 2 > D 1), то I (x 2) < I (x 1).
г) Для обеспечения свойства аддитивности измерительной (метрологической) информации рассмотрим максимальное количество информации, которое можно извлечь из результатов двух независимых неравноточных измерений x 1 и x 2.
Будем искать оценку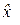 
величины x 0 в линейном виде: 
.
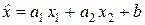Чтобы оценка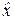 
была несмещённой, то есть чтобы выполнялось равенство 
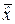= x 0, нужно, чтобы математическое ожидание 
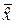оценки 
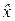было равным измеряемой величине x 0: 
.
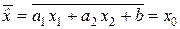Отсюда a 1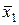 
+ a 2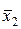 
+ b = x 0, или (a 1 + a 2) x 0 + b = x 0.
Значит, для несмещённости оценки 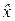следует положить:
b = 0 и a 1 + a 2 = 1.
|
|
|
Определим дисперсию D Σ оценки :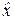
,
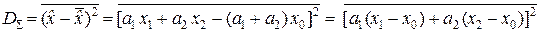или D Σ = a 12 D 1 + a 22 D 2, поскольку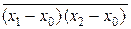 
= 0 – в силу независимо-
сти погрешностей результатов измерений x 1 и x 2.
Введём обозначение a = a 1; тогда a 2 = 1 – a и D Σ = a 2 D 1 + (1 – a) 2 D 2.
Кроме несмещённости оценки 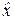разумно также потребовать, чтобы она имела дисперсию, наименьшую из возможных значений дисперсии для линейных оценок вида 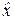= a 1 x 1 + a 2 x 2 (эффективность оценки).
Для этого нужно решить уравнение
dD Σ / da = 2 a D 1 – 2(1 – a) D 2 = 0,
в результате чего находим: a = D 1–1/(D 1–1 + D 2–1) = a 1; a 2 = D 2–1/(D 1–1 + D 2–1);
D Σ–1 = D 1–1 + D 2–1, или σΣ–2 = σ1–2 + σ2–2.
Методом математической индукции можно доказать, что при произволь-
ном значении n > 2 оценки =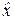 
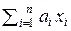будет иметь следующие величины оптимальных весовых коэффициентов { ai } 
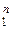и минимальной дисперсии D Σ:
ai = D Σ / Di; D Σ–1 =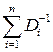 
; σΣ–2 = 
.
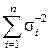Следовательно, в общем случае n независимых неравноточных измерений
(x 1, x 2, …, xi, …, xn) неизвестной величины x 0 её оптимальная оценка 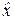вычисляется по формуле: = 
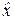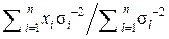и имеет минимально возможную дисперсию D Σ = 
= 
.
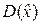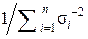| Количественной меройIiизмерительной (метрологической) информации в одномерном случае является обратная дисперсия погрешностей измерительного прибора Ii = 1/ Di, которая удовлетворяет всем четырём постулатам прикладной теории информации. |
Это и есть информационная мера Р. Фишера, которая также представлена на рис. 12.
В 1981 г. Международный комитет мер и весов (МКМВ) рекомендовал использовать как показатель качества измерительной информации неопределённость результата измерения. В 1993 г. Международная организации по стандартизации (ИСО) узаконила в качестве меры неопределённости измерительной информации не энтропию Шеннона или Неймана-Винера, а обычное среднее квадратическое отклонение измеренной величины от среднего значения [47].
Таким образом, простейшая вероятностная модель источника измерительной (метрологической) информации (ИМИ) содержит следующие пять множеств:
U = {– ∞ < x < ∞} – множество возможных значений измеряемой величины;
D = { Dk }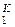 
– множество дисперсий погрешностей измерений Dk (здесь k – но-
мер измерительного прибора);
I = { Ik = 1/ Dk } 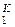– множество количеств информации, вырабатываемой посредством проведения независимых измерений с помощью одного из K измерительных приборов;
P = { Pk } 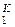– множество вероятностей Pk того, что данное измерение проводилось с помощью k- го прибора (или относительное количество – частотность – измерений, проведённых k- м прибором);
X = {X l (n); n = 1, 2, …; l = 1, 2, …, K n } – множество всевозможных последовательностей (выборок) X l (n) из n неравноточных независимых измерений.
Здесь имеет место полная аналогия со знаковой (синтактической, дискретной) информацией. Более того, так же, как и в знаковой системе, аддитивность информационной меры метрологической информации (Фишера) соблюдается в том случае, если «грамотно» обрабатывать измерительную информацию: в данном случае – правильно взвешивать результаты отдельных измерений xi, чтобы получить оптимальную оценку, для которой и соблюдаются информационные постулаты.
Это аналогично следующему. Чтобы получить на выходе канала передачи дискретной информации (при наличии в канале КПДС помех), то количество знаковой (синтактической) информации, которое соответствует шенноновским оценкам (см. разд. 9), нужно согласовать источник ДИС с каналом КПДС, выработать соответствующие правила присвоения выходным символам значения первичных знаков и провести соответствующее помехоустойчивое канальное кодирование.
Действительно. Пусть имеется l -я выборка X l (n) = (xl 1, xl 2, …, xli, …, xln) объёма n из результатов экспериментальных данных, которые получены различными авторами с помощью приборов, имеющих различную точность измерения. Какое количество метрологической информации I (X l (n)) содержится в собранной нами выборке X l (n)?
Очевидно, что I (X l (n)) =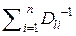 
, а среднее количество информации, приходящееся на одно из n измерений, 
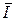(X l (n)) =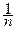 
.
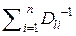При достаточно большом значении n >> 1, аналогично выражению для 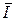(Si (n)) в разд. 8, получаем: 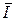(X l (n)) ≈ 
.
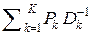Величина 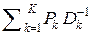не зависит от номера l выборки X l (n) и является собственной информационной характеристикой источника измериттельной (метрологической) информации (ИМИ): {U, D, I, P, X}, которую, по аналогии с источниками знаковых («дискретных») сообщений ДИС, можно назвать средней информативностью результата одного измерения, или удельной информативностью данного источника ИМИ { U, D, I, P, X } и определять её как 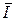(U) = .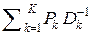
В таком случае для любой, достаточно объёмной (n >> 1), выборки X l (n) получаем асимптотическую оценку количества метрологической информации в этой выборке: I (X l (n)) ≈ n 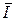(U ) = n .
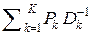Но величина I (X l (n)) есть обратная дисперсия оптимальной линейной оценки 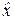измеряемой величины x 0. Дисперсия D Σ этой линейной оценки 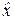асимптотически равна D Σ = 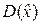≈ 1/[ n 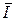(U)].
Если все Dk – одинаковы и равны D, то D Σ ≈ D / n. Этот результат хорошо известен в теоретической метрологии [47] из теории независимых равноточных измерений (аналогия с семиотической мерой Хартли!) и говорит о том, что при n → ∞ дисперсия D Σ линейной оценки =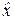 
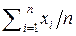теоретически стремится к нулю.
Если выборка (x 1, x 2, …, xi, …, xn) представляет собой статистически связанные между собой случайные величины, то есть результат зависимых неравноточных измерений, то при m = 2 для линейной оценки 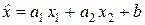имеем: b = 0, a 1 + a 2 = 1 и D Σ = a 12 D 1 + 2 a 1 a 2 R 12+ a 22 D 2, где R 12 – корреляция случайных величин x 1 и x 2; 
.
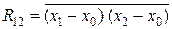Обозначая, как и ранее, a 1 = a, а a 2 = 1 – a, для дисперсии D Σ получаем выражение: D Σ = a 2 D 1 + 2 a (1 – a) R 12+ (1 – a)2 D 2.
Решая уравнение dD Σ / da = 0, получаем
,
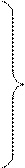
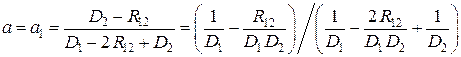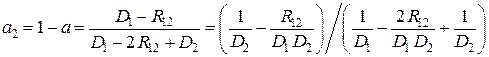, (11.4)
.
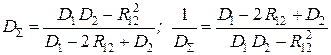Если выборку X(2) = (x 1, x 2) записать в виде числового вектора-столбца x при x Т = || x 1, x 2 || и ввести в рассмотрение корреляционную матрицу R этого случайного вектора x как R = ||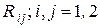 
|| = || 
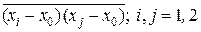||, то матрица R –1, являющаяся обратной к корреляционной матрице R, будет иметь
вид:
.
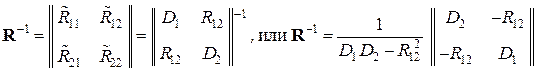Сравнивая выражения для членов матрицы R –1 (11.5), а также для вели-
чин a 1, a 2 и D Σ, видим, что
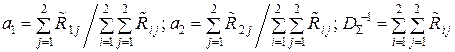. (11.6)
Вид выражения (11.6) не зависит от объёма n выборки X(n). Поэтому мы
сразу же можем записать общее решение для произвольного значения n как
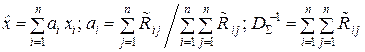. (11.7)
где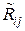 
– i j -й член матрицы R –1, обратной к корреляционной матрице R выборки X(n) = (x 1, x 2, …, xi, …, xn), и доказать справедливость решения (11.7) методом математической индукции по n → ∞.
При этом каждый коэффициент ai в оптимальной оценке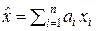 
придаёт соответствующему отсчёту xi относительный вес, пропорциональный той измерительной информации, которую несёт данный отсчёт xi об измеряемой величине x 0. Величина ai пропорциональна сумме членов i -й строки матрицы R –1, обратной к корреляционной матрице R выборки X(n) = (x 1, x 2, …, xi, …, xn), а величину 
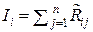можно рассматривать как количество метрологической информации, которое несёт i -й отсчёт xi об измеряемой величине x 0. Тогда в выборке X(n) об измеряемой величине x 0 содержится информации 
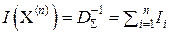, а величину 
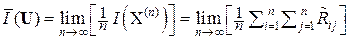следует называть удельной информативностью данного источника метрологической информации ИМИ. Именно поэтому Р. Фишер в 1921 г. (см. разд. 1) назвал матрицу R –1 информационной матрицей выборки X(n) = (x 1, x 2, …, xi, …, xn) из генеральной совокупности { x }.
Количество измерительной информации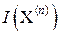 
в достаточно объёмной выборке X(n) (n >> 1) асимптотически равно 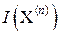≈ n 
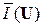. При этом максимальной информативностью 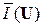обладают (при прочих равных условиях) ис-
точники ИМИ с независимыми равноточными отсчётами. Проверим это утверждение для случая n = 2.
Если x 1 и x 2 – независимы, то R 12 = 0, и при D 1 = D 2 = D имеем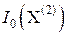 
= = 1/ D 1 + 1/ D 2 = 2/ D. Если R 12 ≠ 0, то
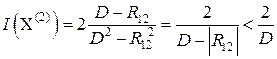, то есть 
< .
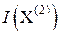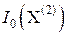Как видим, имеется полная аналогия с информационной статикой дискретных (знаковых) источников сообщений ДИС (см. разд. 4-8), вплоть до удельной информативности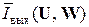 
систем ССПИ при наличии в каналах КПДС помех, если
| в качествеколичественной меры Iiизмерительной (метрологической) информациидля выборки из независимых отсчётов принять обратную дисперсию погрешностей измерительного прибора Ii = 1/ Di, которая удовлетворяетвсем четырём постулатам прикладной теории информации. |
Это и есть информационная мера Р. Фишера (1921 г.), которая также пред-ставлена на рис. 12.
В многомерном случае ситуация несколько усложняется. Рассмотрим результаты измерения координат объекта (x 0, y 0) на плоскости (x, y) – например, с помощью радионавигационной системы.
Пусть погрешности измерений распределены по двумерному гауссовскому закону p (x, y). Этот закон характеризуется дисперсиями погрешностей по осям Ox и Oy (Dx = σ x 2, Dy = σ y 2), а также коэффициентом корреляции ρ xy этих погрешностей.
Самуэль Уилкс (1906-1964) в 1960 г. ввёл понятие обобщённой дисперсии [32]: D у = | R |, где R – корреляционная матрица порядка m погрешностей измерений по переменным xj (j = 1, 2, …, m). В двумерном случае дисперсия Уилкса D у = σ x 2 σ y 2 (1 – ρ xy 2) и равна четвёртой степени радиуса круга r э (эффективного радиуса рассеяния), равновеликого площади единичного эллипса рассеяния погрешностей измерений: r э =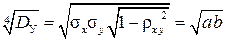 
, где a и b – полуоси единичного эллипса рассеяния.
В то же время, информационная мера Неймана-Винера в этом случае
,
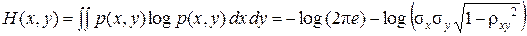то есть h' (x, y) = log r э– 2.
Эта мера удовлетворяет первым трём постулатам теории информации (см. разд. 3), но не четвёртому – постулату аддитивности.
Однако можно проверить, что мера 1/ D У = r э– 4 также не удовлетворяет постулату аддитивности.
Действительно. Пусть ρ xy = 0. В этом простейшем случае, при наличии двух независимых измерений (x 1, y 1) и (x 2, y 2) координат (x 0, y 0) с дисперсиями (σ x 12, σ y 12) и (σ x 22, σ y 22), соответствующие оптимальные оценки по осям Ox и Oy проводятся независимо, так что дисперсии σ x 2 и σ y 2 оптимальных оценок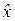 
и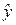 
суть: σ x 2 = 1/(σ x 1– 2 + σ x 2– 2), σ y 2 = 1/(σ y 1– 2 + σ y 2– 2).
При этом эффективные радиусы рассеяния удовлетворяют равенству
r э14 = σ x 12 σ y 12, r э24 = σ x 22 σ y 22, r э4 = σ x 2 σ y 2 = (σ x 1– 2 + σ x 2– 2)– 1 (σ y 1– 2 + σ y 2– 2)– 1,
или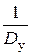 
= 
.
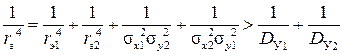Это можно объяснить тем, что в одномерном случае из любого конечного числа отрезков произвольной длины всегда можно составить отрезок суммарной длины; в двумерном случае – из конечного числа квадратов далеко не всегда можно составить квадрат суммарной площади, а в трёхмерном случае – куб суммарного объёма.
Вернёмся к одномерной метрологической информации. Мы видели, что,
несмотря на погрешности измерений некоторой величины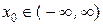 
, с ростом количества n независимых измерений X(n) = (x 1, x 2, …, xi, …, xn) количество измерительной информации в выборке I (X(n)) растёт аддитивно и при оптимальной обработке результатов измерений соответствующая дисперсия 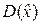оптимальной линейной оценки 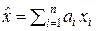величины x 0 уменьшается до бесконечно малой величины: 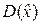→ 0 при n → ∞.
Однако если учесть, что шкала измерительного прибора проградуирована с определённым шагом дискретности Δ x, а аналого-цифровые преобразователи имеют конечную разрядность (цену деления шкалы Δ x), то возникает вопрос, c какой предельно достижимой точностью можно измерить величину x 0 в результате достаточно большого количества многократных независимых измерений (проблема округления)?
Пусть некоторая действительная величина 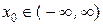измеряется с помощью прибора, проградуированного с шагом дискретности Δ x или выдающе-го результаты измерений с округлением по правилу 
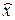= [ x /Δ x + 0,5 ] Δ x, где символ [ y ] обозначает целую часть некоторого действительного числа y. Поскольку мы заранее, естественно, не знаем значения величины x 0 с достаточной точностью, то можно считать, что в пределах цены деления x I < x 0 ≤ x II априорное распределение неизвестной величины x 0 является равномерным (см. рис. 13).
Поэтому если в качестве результата однократного измерения величины x 0 мы получили значение x 1 = x I, то величина x 0 имеет апостериорное распределение p I(x), приблизительно равномерное в пределах промежутка:
(x I – Δ x /2) < x ≤ (x I + Δ x /2).
p (x)
 |
p I (x)
p 0 (x)
Δ x
0 x I x 0 x II x
Рис. 13. Априорная p 0(x) и апостериорная p I(x)
плотности вероятности величины x 0
Отсюда среднее значение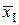 
и дисперсия D I результата однократного измерения суть:
,
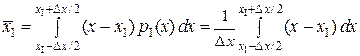или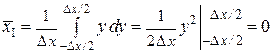 
;
,
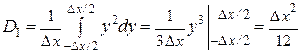или D I/Δ x 2 = 1/12, σI =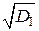 
≈ 0,288 Δ x, где y = x – x I.
Если мы проведём серию из n независимых измерений, то в результате округления получим выборку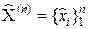 
, имеющую вид 
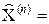(x I, x I, …, x I).
Значит, оптимальная оценка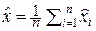 
= x I останется по-прежнему несмещённой, но будет иметь ту же дисперсию D Σ = Δ x 2/12, то есть неопределённость оценки 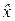не уменьшается с увеличением объёма выборки n.
Интуитивно это вполне понятно: сколько ни производи повторных измерений, а с помощью школьной линейки не получить микронной точности!
Но тогда возникает метрологическая задача: сколько нужно провести сеансов измерений величины x 0 при наличии случайных помех измерениям с помощью данного измерительного прибора, имеющего цену деления шкалы Δ x, чтобы реализовать точность этого прибора?
Для рассмотренной нами информационной меры Р. Фишера эта задача решается элементарно. Поскольку предельная информативность прибора ограничивается дискретностью Δ x, то есть величиной I мин = 12 /Δ x 2, а удельная информативность процедуры измерения составляет величину 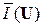, то необходимое количество процедур n определяется уравнением:
I мин = n 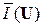, или 12/Δ x 2 = n .
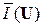Отсюда получаем n ≥ 12/[ 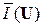Δ x 2].
Например, если помехи приводят к независимым равноточным результатам измерений x 1, x 2, …, xn величины x 0 с априорной неопределённостью σ0, то 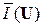= σ0–2, а потому n ≥ 12 (σ0 /Δ x) – 2.
Вопросы для самопроверки
1. Какое противоречие возникает при формально-математическом обобщении энтропии источника дискретных сообщений на источники измерительной (метрологической) информации?
2. Каковы особенности дифференциальной энтропии источника измерительной (метрологической) информации?
3. Каковы основные постулаты для измерительной (метрологической) информации?
4. Что является количественной мерой измерительной (метрологической) информации?
5. Что такое обобщённая дисперсия Уилкса?
6. Каким образом решается информационная проблема округления в теоретической метрологии?
