Методические указания. Для степени с рациональным показателем n

Для степени с рациональным показателем n:

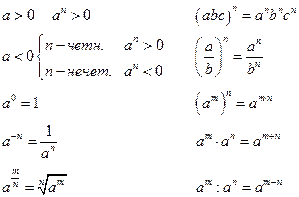
Уравнения, содержащие неизвестную переменную в показателе степени, называются показательными уравнениями.

При решении показательных уравнений используется условие равенства двух степеней: две степени равны тогда и только тогда, когда равны основания степеней и их показатели.

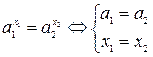
Рассмотрим решение нескольких примеров:

1.

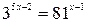
В основе решения данного уравнения лежит условие равенства 2 степеней. Уравняем основания степеней:

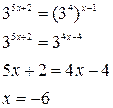
Ответ: - 6

2.

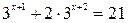
Так как числовые коэффициенты при х равны, то в основе решения данного уравнения лежит разложение левой части на множители. За скобку выносится общий множитель – степень с наименьшим показателем, Чтобы узнать, что останется в скобке, нужно каждую степень разделить на общий множитель.

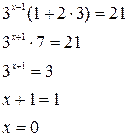
Ответ: 0.

3.

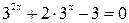
Так как числовые коэффициенты при х не равны, то в основе решения данного уравнения лежит введение новой переменной, позволяющей показательное уравнение заменить квадратным алгебраическим.

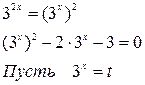
Тогда

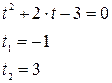
Получили: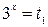

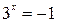- не подходит, так как степень всегда положительна (а^х >0)

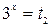
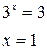
Ответ: 1.