При нагружении цилиндрической тонкостенной оболочки внутренним давлением 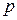 в ней возникают меридиональные
в ней возникают меридиональные 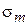 и кольцевые
и кольцевые 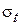 напряжения. Тонкостенными считаются те оболочки, у которых толщина стенки не превышает 10% их внутреннего диаметра, а рабочее давление не более 10 МПа /6/.
напряжения. Тонкостенными считаются те оболочки, у которых толщина стенки не превышает 10% их внутреннего диаметра, а рабочее давление не более 10 МПа /6/.
По безмоментной (мембранной) теории расчета меридиональные и кольцевые напряжения, действующие по срединной поверхности тонкостенной цилиндрической обечайки, вычисляются по формулам:
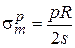 ; (1)
; (1)
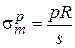 . (2)
. (2)
где 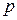 – расчетное давление;
– расчетное давление; 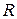 ,
, 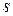 – радиус срединной поверхности и толщина оболочки
– радиус срединной поверхности и толщина оболочки
Моментная теория расчета в дополнение к растягивающим и сжимающим усилиям учитывает действие на обечайку поперечных сил и изгибающих моментов. В связи с этим в расчетных формулах для напряжений появляются дополнительные слагаемые, что будет показано ниже.
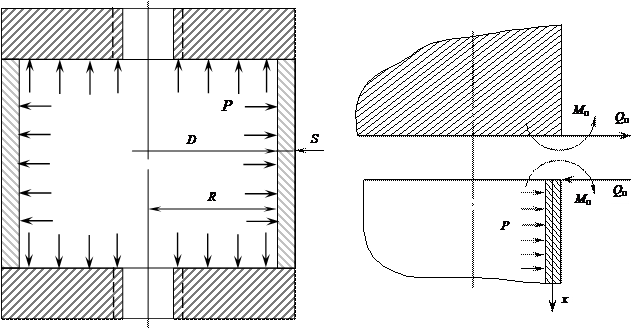
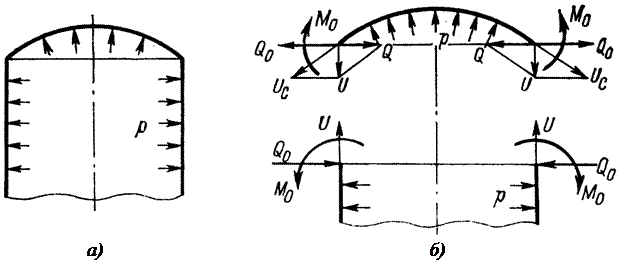
Экспериментальная цилиндрическая оболочка, в которой определяются напряжения, представляет собой вертикальную цилиндрическую обечайку, сваренную по краям с массивными плоскими днищами (рис. 1, а). При теоретическом анализе такая цилиндрическая оболочка может рассматриваться как жестко связанная с недеформирующимися основаниями. На эквивалентной схеме сопряжения цилиндрической оболочки и плоского днища (рис. 1, б) показаны равномерно распределенные по краям оболочек краевая сила 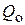 и краевой момент
и краевой момент 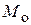
 |
а) б)
Рис.1. Экспериментальная цилиндрическая оболочка (а) и эквивалентная схема
сопряжения цилиндрической оболочки и плоского днища (б)
В общем случае в узле сопряжения различных элементов оболочек (например, цилиндрической и сферической) действуют внутреннее давление 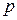 и равномерно распределенные по краям оболочек краевая сила
и равномерно распределенные по краям оболочек краевая сила 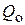 и краевой момент
и краевой момент 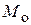 (см. рис. 2).
(см. рис. 2).
В том случае, когда имеет место соединение частей оболочек под углом друг к другу, в месте соединения возникает еще одна краевая сила – распорная сила 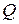 (она является проекцией меридиональной силы
(она является проекцией меридиональной силы 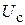 , возникающей на краю оболочки под действием давления; другой проекцией является сила
, возникающей на краю оболочки под действием давления; другой проекцией является сила 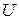 ).
).
Для определения 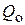 и
и 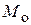 составляют уравнения совместности радиальных
составляют уравнения совместности радиальных 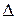 и угловых
и угловых  деформаций. При определении знаков деформаций рассматриваются сечения оболочки, расположенные справа от оси. При этом используется следующее правило: радиальные перемещения
деформаций. При определении знаков деформаций рассматриваются сечения оболочки, расположенные справа от оси. При этом используется следующее правило: радиальные перемещения 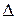 края оболочки считаются положительными, если под воздействием нагрузки происходит увеличение радиуса оболочки; угловые перемещения
края оболочки считаются положительными, если под воздействием нагрузки происходит увеличение радиуса оболочки; угловые перемещения 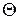 считаются положительными, если поворот края оболочки происходит по часовой стрелке. Это правило знаков.
считаются положительными, если поворот края оболочки происходит по часовой стрелке. Это правило знаков.
 |
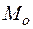 (рис. 2).
(рис. 2).
Рис. 2. Схема к определению краевых сил и моментов:
а – соединение сферической и цилиндрической оболочек; б – расчетная схема;
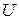 и
и 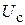 – меридиональные усилия соответственно цилиндрической и сферической оболочек
– меридиональные усилия соответственно цилиндрической и сферической оболочек
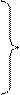 С учетом этого правила для правой относительно оси части оболочек (рис. 2, б) составляются уравнения:
С учетом этого правила для правой относительно оси части оболочек (рис. 2, б) составляются уравнения:
|
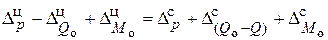
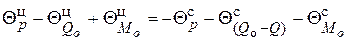 .
.
Индексы «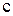 » и «
» и «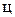 » относятся к составляющим частям оболочек: цилиндрической и сферической.
» относятся к составляющим частям оболочек: цилиндрической и сферической.
Индексы внизу указывают, что деформации происходят под действием соответственно давления 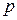 , распорных сил
, распорных сил 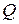 , краевой силы
, краевой силы 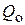 и краевого момента
и краевого момента 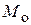 . Причем индексы
. Причем индексы 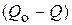 указывают, что деформации происходят под действием алгебраических сумм краевых и распорных сил, при этом распорные силы в обеих частях оболочек могут быть различными.
указывают, что деформации происходят под действием алгебраических сумм краевых и распорных сил, при этом распорные силы в обеих частях оболочек могут быть различными.
В случае если нагруженная цилиндрическая оболочка жестко закреплена в недеформирующемся основании (рис. 1), распорная сила отсутствует. При этом уравнения (3) упрощаются и с учетом того же правила знаков принимают вид:
|
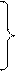
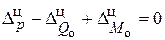
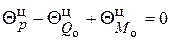
Радиальные 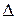 и угловые
и угловые 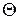 деформации цилиндрической оболочки, входящие в уравнение (4), определяются для края оболочки (расстояние
деформации цилиндрической оболочки, входящие в уравнение (4), определяются для края оболочки (расстояние 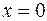 ) по формулам [4]:
) по формулам [4]:
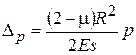 ;
; 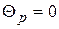 ;
;
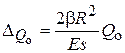 ;
; 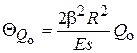 ; (5)
; (5)
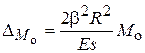 ;
; 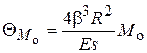 ,
,
где 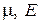 – коэффициент Пуассона и модуль упругости материала оболочки;
– коэффициент Пуассона и модуль упругости материала оболочки; 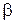 – коэффициент затухания
– коэффициент затухания
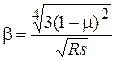 . (6)
. (6)
Подставляя значения деформаций (5) в уравнения (4) и решая их, получим величину краевой силы 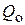 и краевого момента
и краевого момента 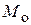 :
:
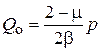 ;
; 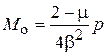 . (7)
. (7)
Суммарные меридиональные 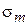 и кольцевые
и кольцевые 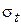 напряжения, возникающие в стенке цилиндрической оболочки, составляют:
напряжения, возникающие в стенке цилиндрической оболочки, составляют:
меридиональные
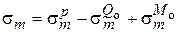 ;
;
кольцевые (8)
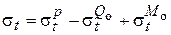 ,
,
где 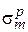 ,
, 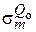 ,
, 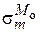 ,
, 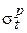 ,
, 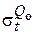 ,
, 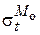 – меридиональные и кольцевые напряжения, возникающие в оболочке от действия соответствующих нагрузок:
– меридиональные и кольцевые напряжения, возникающие в оболочке от действия соответствующих нагрузок: 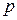 ,
, 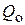 ,
, 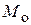 .
.
Знак «плюс» при напряжениях от давления 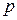 и краевого момента
и краевого момента 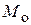 и знак «минус» от краевой силы
и знак «минус» от краевой силы 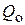 соответствуют указанному ранее правилу знаков.
соответствуют указанному ранее правилу знаков.
Меридиональные и кольцевые напряжения на самом краю цилиндрической оболочки (х = 0) составляют [3, 4]:
|
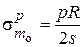 ;
; 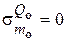 ;
; 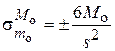 ;
; 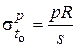 ;
; 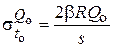 ;
; 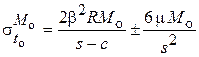 .
.
Здесь знаки напряжений от краевого момента 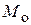 указывают, что на внутренней поверхности оболочки волокна растянуты (+), а на наружной поверхности сжаты (–).
указывают, что на внутренней поверхности оболочки волокна растянуты (+), а на наружной поверхности сжаты (–).
Напряжения на расстоянии 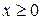 от края оболочки могут быть вычислены с учётом решения для краевой задачи [2, 4, 5]. Суммарные меридиональные и кольцевые напряжения в соответствии с формулами (8) для наружной поверхности экспериментальной цилиндрической оболочки на расстоянии
от края оболочки могут быть вычислены с учётом решения для краевой задачи [2, 4, 5]. Суммарные меридиональные и кольцевые напряжения в соответствии с формулами (8) для наружной поверхности экспериментальной цилиндрической оболочки на расстоянии 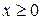 от её края равны:
от её края равны:
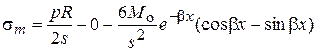 ;
;
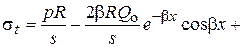 (10)
(10)
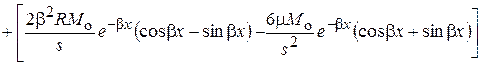 .
.
 2015-06-10
2015-06-10 2158
2158








