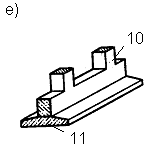
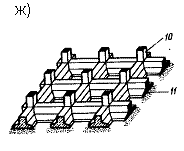
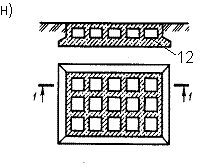
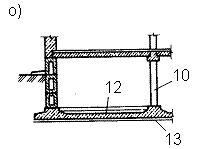
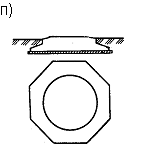
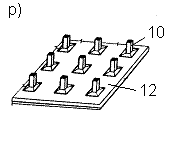
К гибким фундаментам относятся все ленточные железобетонные фундаменты, фундаменты из монолитного железобетона под отдельные опоры или группы опор (рис. 7 е), фундаменты из перекрестных лент (рис. 7 ж), коробчатые плиты (если необходимо воспринять очень большие изгибающие моменты, возникающие в сплошных плитах, например у фундаментов высотных зданий) (рис. 7 н), круглые (рис. 7 г) или кольцевые (рис. 7 п) в плане плиты, сплошные железобетонные плиты под колонны(рис. 7 р).
На усилия в конструкции гибкого фундамента влияет его жесткость, жесткость основания и жесткость надземных конструкций.
В зависимости от протяженности гибких фундаментов различают плоскую задачу, когда фундамент в каждом сечении по его длине имеет одинаковую форму деформации и пространственную задачу в двух случаях: 1. балка на упругом основании. 2. фундаментная плита на упругом основании.
Теория местных деформаций: реакция грунта основания в каждой точке подошвы фундамента (балки) прямо пропорциональна осадке этой точки, т.е. py=CzZ
Cz – коэффициент постели (упругого сжатия основания); Z – осадка в месте определения реакции грунта py.
Теория упругого пространства является другой крайней теорией расчета балок и плит на упругом основании. В этом случае фундаментная балка принимается лежащей на однородном упругом или линейно деформируемом бесконечном полупространстве.
Теория расчета балок на упругом (линейно деформируемом) слое грунта конечной толщины. Основной сложностью использования этой теории является установление толщины деформируемого слоя. Это можно сделать, руководствуясь способом определения расчетной мощности сжимаемой толщи при расчете осадки фундаментов методом ограниченной фундаментной толщи.
При предварительном подборе сечения балки на упругом основании обычно принимают равномерное или трапециевидное распределение давления по подошве.
 2015-06-26
2015-06-26 4224
4224








