x=2sin7(t), y=-4.5cos(t)(1+1.2cos(t))+(cos2(t)1/8+2.5
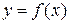 – у есть образ элемента х при данном отображении f.
– у есть образ элемента х при данном отображении f.
Прообраз элемента у – это совокупность тех элементов 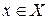 , образом которых является элемент
, образом которых является элемент 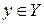 . Обозначается
. Обозначается 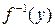 .
.
Образ множества 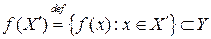 .
.
Полный прообраз множества 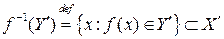 .
.
Отображение f cюръективно, если каждый элемент множества У имеет прообраз.
Отображение f инъективно, если для каждого элемент 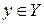 существует не более одного прообраза, т.е. для любых
существует не более одного прообраза, т.е. для любых 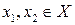 , если
, если 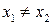 , то
, то 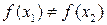 .
.
Если отображение f cюръективно и инъективно, то оно биективно.
Биективное отображение – это взаимно однозначное соответствие.
Обратное отображение 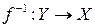 , определяется для биекции
, определяется для биекции 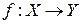 следующим образом: если
следующим образом: если 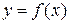 , то
, то 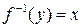 ,
, 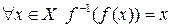 ,
, 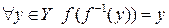 .
.
Если 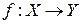 ,
, 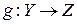 , то их композицией(произведением) называют отображение
, то их композицией(произведением) называют отображение 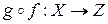 , определяемое формулой
, определяемое формулой 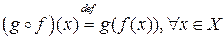 .
.
Свойства композиции
1. 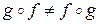
2. 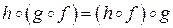
Декартовым произведением множеств Х и У называется множество 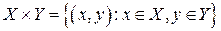 .
.
Квадратом множества А называют декартово произведение множества на само себя: 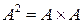 .
.
Бинарным отношением 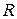 в множестве А будем называть подмножество его квадрата
в множестве А будем называть подмножество его квадрата 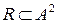 .
.
Примеры.
1. Отношение 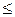 выполняется для пар
выполняется для пар 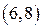 и
и 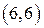 , и не выполняется для
, и не выполняется для 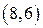 .
.
2. Отношение «иметь общий делитель, отличный от 1» выполняется для пар 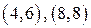 , но не выполняется для
, но не выполняется для 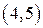 .
.
Отношением эквивалентности называется всякое отношение 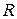 , которое удовлетворяет трем условиям:
, которое удовлетворяет трем условиям:
1. Рефлексивности: 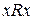 . 2. Симметричности: если
. 2. Симметричности: если 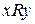 , то и
, то и 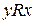 . 3.Транзитивности: если
. 3.Транзитивности: если 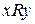 и
и 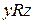 , то и
, то и 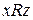
 2015-06-26
2015-06-26 247
247






