W(p)= 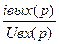 =
= 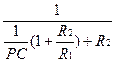 =
= 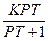 , (1.2.5)
, (1.2.5)
где K= 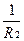 - коэффициент ослабления информационного сигнала,
- коэффициент ослабления информационного сигнала,
T=C 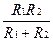 - постоянная времени звена.
- постоянная времени звена.
при R1>>R2
K= 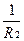 ; T=CR2. (1.2.6)
; T=CR2. (1.2.6)
1.3. Интегрирующее звено
Принципиальная схема интегрирующего звена приведена на рис. 1.3.1 [2]:
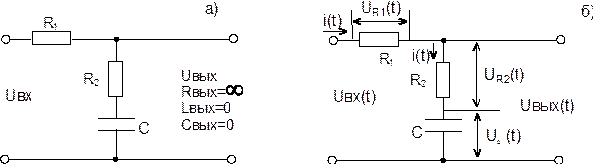
Рис. 1.3.1. Принципиальная схема (а) и схема распределения падений напряжений на элементах интегрирующего звена (б).
Система уравнений интегрирующего звена рис. 1.3.1а а изображениях по Лапласу записывается в следующем виде [2]:
Uвх(p)=i(p)R1+Uвых(p),
Uвых(p)=i(p)R2+i(p) 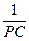 . (1.3.1)
. (1.3.1)
Подставляя в первое уравнение (1.3.1) второе, получим систему уравнений
Uвх(p)=i(p)R1+i(p)R2+i(p) 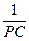 ,
,
Uвых(p)=i(p)R2+i(p) 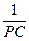 . (1.3.2)
. (1.3.2)
Отсюда получаем выражение для передаточной функции
W(p)= 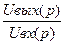 =
= 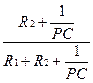 . (1.3.3)
. (1.3.3)
При R1>> 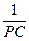 и R2£
и R2£ 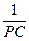 из выражения (1.3.3) получаем
из выражения (1.3.3) получаем
W(p)= 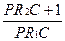 =
= 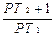 , (1.3.4)
, (1.3.4)
где T2=R2C – постоянная времени форсирования;
T=R1С – постоянная времени интегрирования.
1.4. Колебательное звено
Принципиальная схема колебательного звена приведена на рис. 1.4.1 [2].
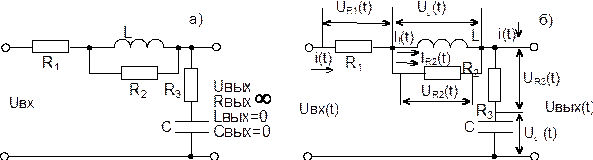
Рис. 1.4.1. Принципиальная схема (а) и схема распределения падений напряжений (б) на элементах колебательного звена.
Система уравнений колебательного звена рис. 1.4.1 в изображениях по Лапласу записывается в следующем виде [2]:
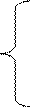 |
Uвх(p)=i(p)R1+iL(p)PL+Uвых(p),
Uвых(p)=i(p)R3+i(p) 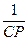 ,
,
i(p)=iR2(p)+iL(p), (1.4.1)
iR2(p)R2=iL(p)PL.
Так как во втором уравнении (1.4.1) Uвых(p) выражается через неизвестный ток i(p), то выразим через этот параметр значение тока iL(p) для того, чтобы подставить в первое уравнение(1.4.1) и только бы там остался неизвестный ток i(p). Предварительно решим третье и четвертое уравнение (1.4.1) относительно тока iL(p):
i(p)=iL(p) 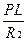 +iL(p)=iL(p)
+iL(p)=iL(p) 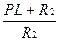 (1.4.2)
(1.4.2)
или
iL(p)=i(p) 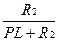 . (1.4.3)
. (1.4.3)
Далее подставляя выражение (1.4.3) для iL(p) в первое уравнение (1.4.1), получим систему уравнений:
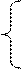 Uвх(p)=i(p)(R1+
Uвх(p)=i(p)(R1+ 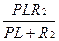 +R3+
+R3+ 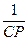 ), (1.4..4)
), (1.4..4)
Uвых(p)=i(p)(R3+ 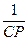 ).
).
Из системы уравнений (1.4.4) получаем выражение для передаточной функции колебательного звена по соотношению (1):
W(p)= 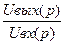 =
= 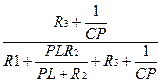 , (1.4.5)
, (1.4.5)
при R3<< 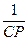 , R1»R3 и R2>>PL
, R1»R3 и R2>>PL
W(p)= 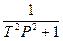 , (1.4.6)
, (1.4.6)
где T= 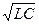 - постоянная времени колебательного звена.
- постоянная времени колебательного звена.
при R2>>PL и R1»R3
W(p)= 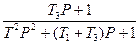 =
= 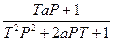 , (1.4.7)
, (1.4.7)
где T1=R1C; T3=R3C; a= 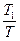 -коэффициент затухания.
-коэффициент затухания.
 2015-06-26
2015-06-26 494
494








