Математическое ожидание ДСВ Х принимающей конечное множество значений с законом распределения
p(X=xk)=pk; k=1,2,3,…,n (1)
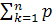 k=1 (2)
k=1 (2)
называется сумма произведений ее значений на их соответствующие вероятности
M(x) = x1*p1+x2*p2+…+xn*pn
M(x) = 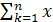 kpk
kpk
В мат. ожидании ДСВ приближенно равно среднему арифметическому всех ее возможных значений. В следствие этого мат. ожидание СВ называют его средним значением.
Замечание:
Мат. ожидание СВ называют так же центром распределения. Это название заимствовано из механики и объясняется следующим:
- если в точках x1, x2,…,xn оси Ox находятся соответственно массивы p1,p2,…,pn, то координата x центра тяжести системы материальных точек вычисляется по формуле:

 X =
X = 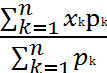 мат. ожидание
мат. ожидание
вероятность
Замечание:
Поскольку выполняется 2, то X = 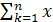 kpk = M(x)
kpk = M(x)
Мат. ожидание ДСВ принимающей бесконечную последовательность значений с законом распределения
p(X-xk) = pk; k=1,2,3,… (4)
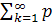 k=1 (5)
k=1 (5)
M(x)=x1p1+x2p2+…
M(x)= 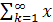 kpk (6)
kpk (6)
Определяется формулой 6 если ряд сходится абсолютно.
Мат. ожидание непрерывной СВ Х, все значения которой принадлежат отрезку [α; β], а p(x) – ее плотность вероятности определяется формулой:
M(x)= 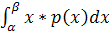 (7)
(7)
Если все значения непрерывной СВ X принадлежат бесконечному промежутку (-∞;+∞) а p(x) – ее плотность вероятности, то мат. ожидание определяется формулой:
M(x)= 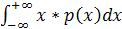 (8)
(8)
Когда этот несобственный интеграл сходится абсолютно. Мат. ожидание СВ есть величина постоянная
Свойства математического ожидания:
1) Значение мат. ожидания СВ X заключено между ее наименьшим и наибольшим значениями:
a ≤ M(x) ≤ b (9), где a – наименьшее, b – наибольшее
2) Мат. ожидание постоянной величины равно этой величине:
M(C) = C, C=const (10)
3) Постоянный множитель можно вынести за знак мат. ожидания:
M(CX) = C*M(X), C=const (11)
4) Мат. ожидание суммы двух СВ равно сумме их мат. ожиданий:
M(X+Y) = M(X) + M(Y) (12)
это равенство распространяется на n случайных величин:
M(x1+x2+…+xn) = M(x1) + M(x2) +…+ M(xn) (13)
5) Мат. ожидание разности двух СВ равно разности их мат. ожиданий:
M(X-Y) = M(X) – M(Y) (14)
6) Мат. ожидание произведения двух независимых СВ равно произведению мат. ожиданий этих величин:
M(X*Y) = M(X) * M(Y) (15)
это равенство распространяется на n независимых С:
M(x1*x2*…*xn) = M(x1) * M(x2) *…* M(xn) (16)
Пример 1: Найти мат. ожидание ДСВ X, закон распределения которой задан таблицей
| x | |||||
| p | 0,1 | 0,2 | 0,4 | 0,2 | 0,1 |
Решение:
В соответствии с формулой 3 находим:
M(x) = 3*0,1 + 4*0,2 + 5*0,4 + 6*0,2 + 7*0,1 = 5
Итак мат. ожидание данной СВ=5
3 < 5 < 7
a < M(x) <b
неравенство 9 выполняется.
Пример 2: Закон распределения ДСВ задан таблицей:
| x | -4 | -2 | |||
| p | 0,1 | 0,2 | 0,15 | 0,25 | 0,3 |
Записать закон распределения СВ: 3x;  .
.
Найти мат. ожидание СВ: x;3x; 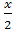
Решение:
Запишем законы распределения СВ 3x и  с помощью таблицы. По формулам 3 вычислим мат. ожидание этих величин:
с помощью таблицы. По формулам 3 вычислим мат. ожидание этих величин:
| 3x | -12 | -6 | |||
| p | 0,1 | 0,2 | 0,15 | 0,25 | 0,3 |
M(3x)

| -2 | -1 | |||
| P | 0,1 | 0,2 | 0,15 | 0,25 | 0,3 |
M( )
)
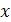
| -4 | -2 | |||
| p | 0,1 | 0,2 | 0,15 | 0,25 | 0,3 |
M(x)
M(x) = -4*0,1-2*0,2+0*0,15+2*0,25+4*0,3 = 0,9
M(3x) = -12*0,1-6*0,2+0*0,15+6*0,25+12*0,3 = 2,7
M( ) = 0,45
) = 0,45
Замечание: мат. ожидание СВ 3x и  можно выполнить пользуясь равенством 11 при известном мат. ожидании величины X:
можно выполнить пользуясь равенством 11 при известном мат. ожидании величины X:
M(3x) = 3M(x) = 3*0,9 = 2,7
M( *x) =
*x) =  * M(x) = 0,45.
* M(x) = 0,45.
 2015-06-28
2015-06-28 292
292







