Даны вершины треугольника M1M2M3: М1(-3;0), M2(2;5), M3(3;2).
а) Найти периметр треугольника, вершинами которого служат середины сторон.
б) Найти периметр треугольника, вершинами которого служат основания высот, проведенных из вершин M1 M2 M3 к противоположным сторонам.
в) Найти периметр треугольника, вершинами которого служат основания биссектрис, проведенных из вершин M1 M2 M3 к противоположным сторонам.
Решение.
а) Построение:
К, Е, F – середины соответствующих сторон М1М3, М1М2, М2М3.
| F |
| E |
| K |
| M1 |
| M2 |
| M3 |
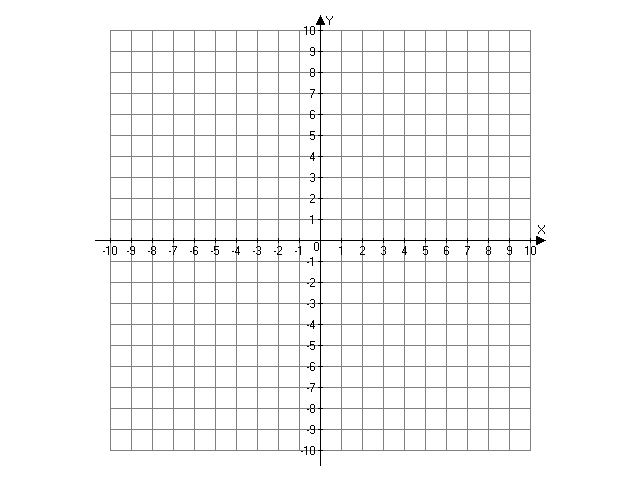
К – середина М1М3, тогда координаты середины стороны будут:
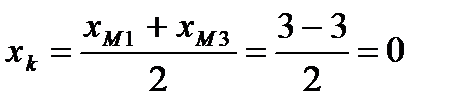
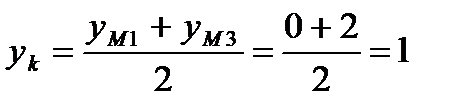
Тогда К(0;1).
Е – середина М1М2, тогда координаты середины стороны будут:
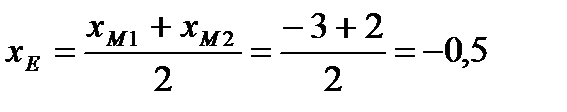
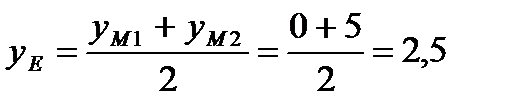
тогда Е(-0,5; 2,5).
F – середина М2М3, тогда координаты середины стороны будут:
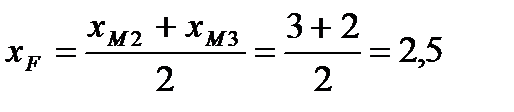 .
.
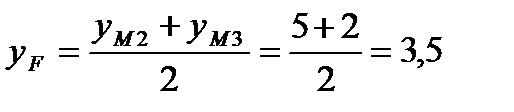
тогда F(2,5; 3,5).
KF= 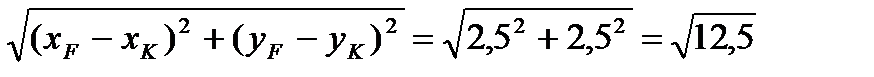
Аналогично: EF= 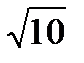 ; EK=
; EK= 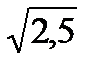 . Тогда периметр треугольника будет:
. Тогда периметр треугольника будет: 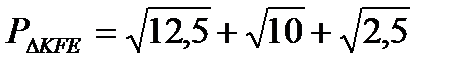
б)
| M1 |
| M2 |
| M3=N=M |
| K |
 Где М1?
Где М1? Покажем, что треугольник прямоугольный и его три высоты не могут составить замкнутую фигуру.
Найдем уравнение стороны М1М2:
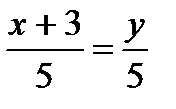 откуда имеем
откуда имеем
5x+15=5y; y=x+3. Хорошо видно, что угловой коэффициент этой прямой k1=1, а
т. к. высота М3К перпендикулярна стороне М1М2, то k2 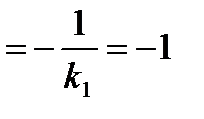
Используя уравнение прямой через точку: у-y1=k(x-x1) имеем
M3K:
y-2=-1(x-3), y-2=-x+3 откуда получаем y+x-5=0.
Уравнение пучка прямых:
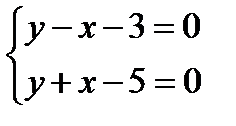 .
.
2y=8,
y=4, то x=1, тогда М3К  М1М2=К(1;4).
М1М2=К(1;4).
Найдем уравнение стороны М2М3:
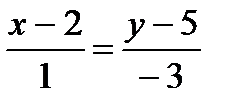 .
.
-3x+6=y-5, y=-3x+11, откуда видно что угловой коэффициент этой прямой k1=-3,
т. к. М1N перпендикуляреныМ2М3, k2 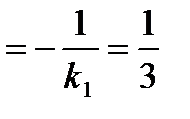
тогда уравнение стороны М2М3 будет
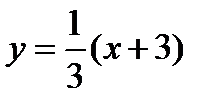 , 3y-x-3=0
, 3y-x-3=0
Уравнение пучка прямых:
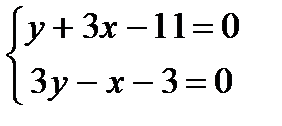 .
.
у=11-3x, 33-9x-x-3=0. x=3 y=2, то x=3,
тогда М1N  М2М3=N(3;2).
М2М3=N(3;2).
Найдем уравнение стороны М1М3:
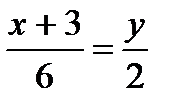 .
.
2x+6=6y, 3x-x-3=0,
y= 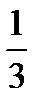 x+1, k1=
x+1, k1= 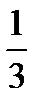 , то k2
, то k2 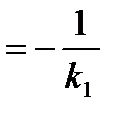 т. к. М2M перпендикулярна М1М3, k2=
т. к. М2M перпендикулярна М1М3, k2= 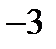 . Найдем уравнение стороны М1N:
. Найдем уравнение стороны М1N:
y-5=-3(x-2), y-5=-3x+6, y+3x-11=0.
Уравнение пучка прямых:
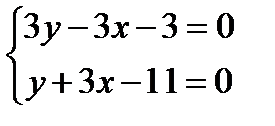 .
.
y=2, то x=3,
тогда М2M  М1М3=N(3;2).
М1М3=N(3;2).
Имеем:
KN= 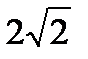 ; КM=
; КM= 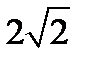 ; NM=0; т.е. мы доказали, что
; NM=0; т.е. мы доказали, что
ΔКNM не существует
в)Построение: М1А, М2В и М3С – биссектрисы углов при вершинах М1М2 М3
| A |
| C |
| B |
| M3 |
| M2 |
| M1 |
Найти периметр треугольника АВС
1) 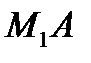
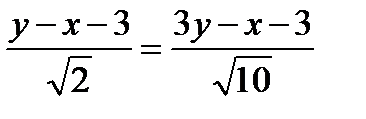 .
.
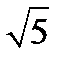 (у-х-3)=3у-х-3;
(у-х-3)=3у-х-3;
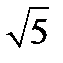 у-
у- 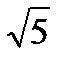 х-3
х-3 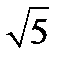 =3у-х-3;
=3у-х-3;
у(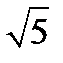 -3)+х(-
-3)+х(- 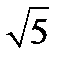 +1)+(3-3
+1)+(3-3 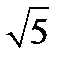 )=0 - уравнение биссектрисы
)=0 - уравнение биссектрисы 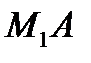
2) 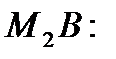
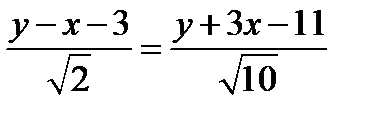 .
.
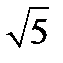 (у-х-3)=у+3х+11;
(у-х-3)=у+3х+11;
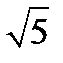 у-
у- 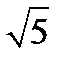 х-3
х-3 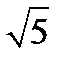 =у+3х+11;
=у+3х+11;
у(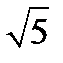 -1)+х(-
-1)+х(- 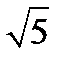 -3)+(-3
-3)+(-3 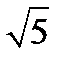 +11)=0 - уравнение биссектрисы
+11)=0 - уравнение биссектрисы 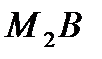
3) 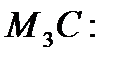
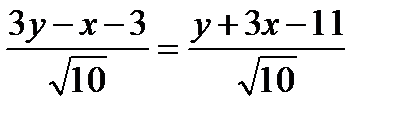 .
.
3у-х-3=у+3х-11;
2у-4х+8=0 - уравнение биссектрисы 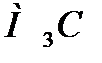
Найдем основания биссектрис, как точки пересечения сторон треугольника и с ответствующей биссектрисы:
1) 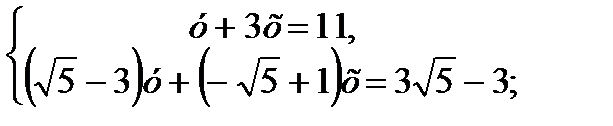
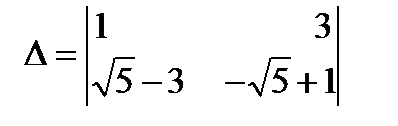 =-4
=-4 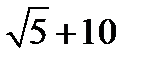 ;
;
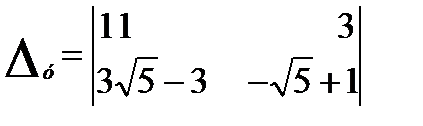 =-20
=-20 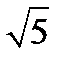 +20;
+20;
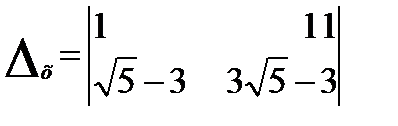 =
= 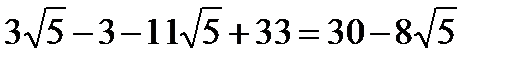
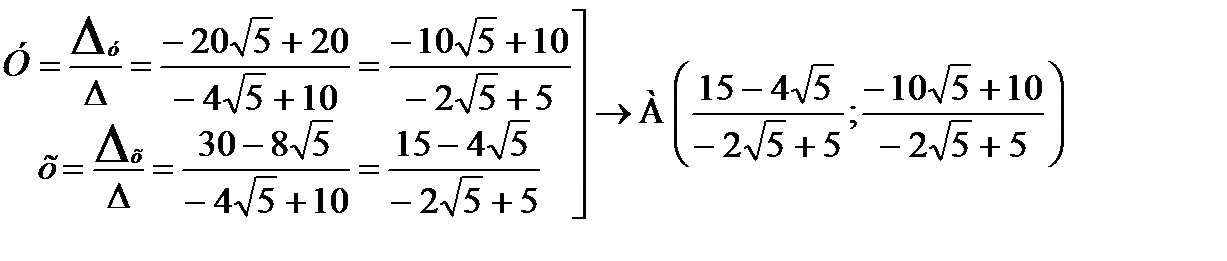 .
.
2) 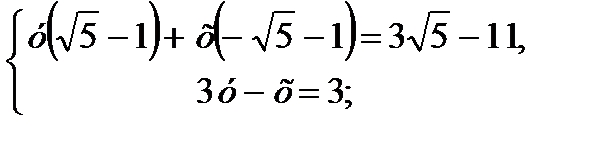
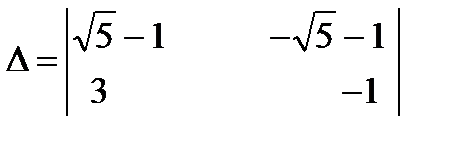
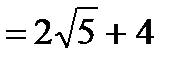 ;
;
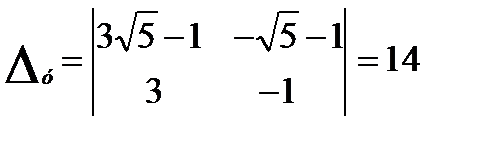 ;
;
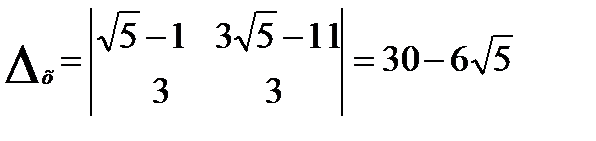 .
.
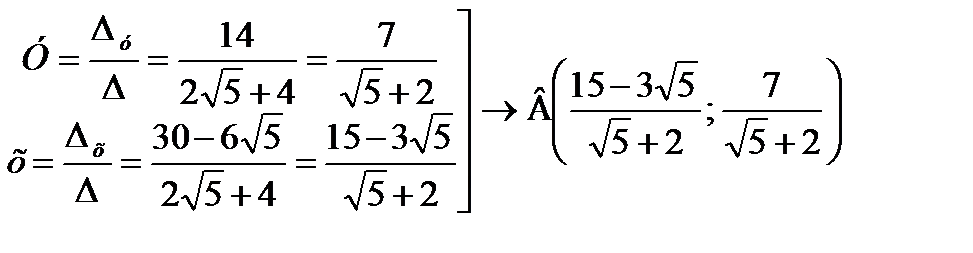 .
.
3) 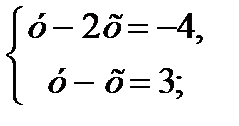
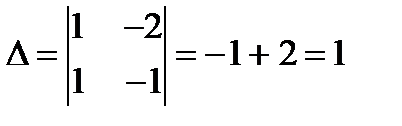 .
.
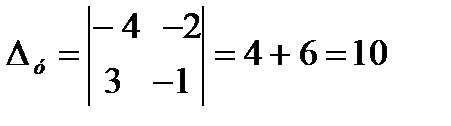
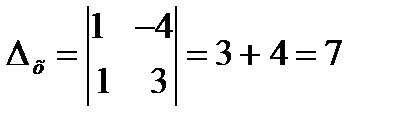
у =10, х=7 Следовательно С(7,0)
Найдем 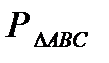
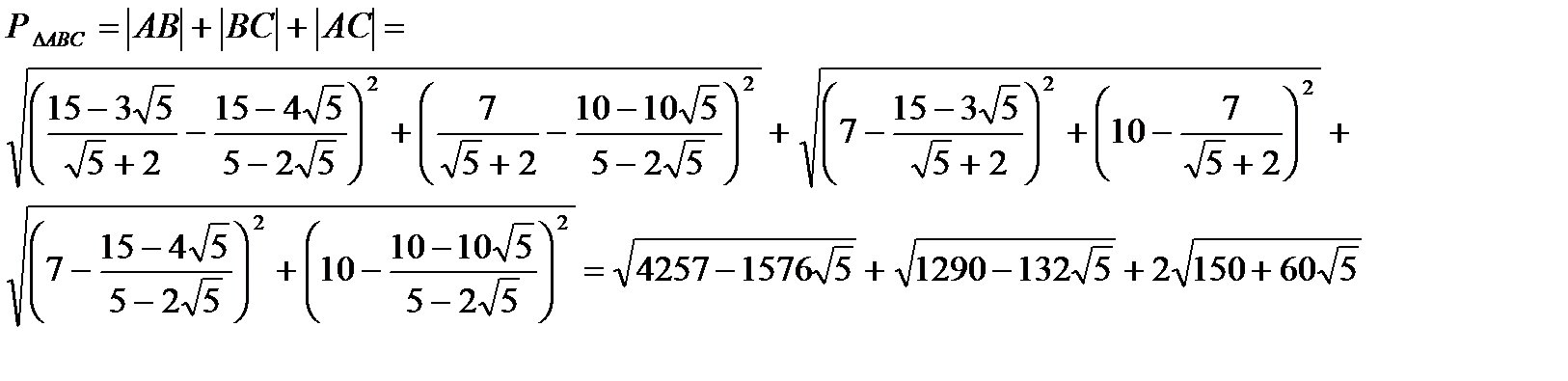
Задача №4
Даны вершины равнобедренного треугольника 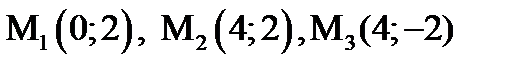
а)Доказать, что середины сторон равнобедренного треугольника являются также вершинами равнобедренного треугольника.
б) Доказать, что биссектриса, проведенная из вершины при основании равны.
в) Медианы, проведенные из вершин при основании равны.
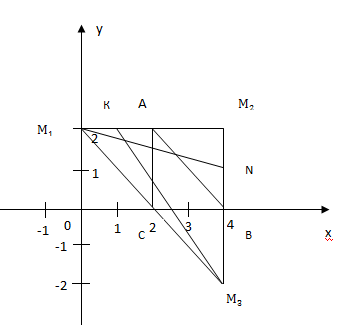
а)Дано: ΔАВС
Доказать, что середины сторон равнобедренного треугольника являются также вершинами равнобедренного треугольника.
Доказательство.
Найдем середины сторон треугольника
1) Найдём середину отрезка A 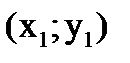
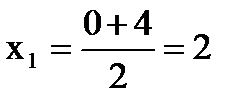
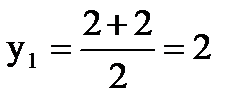
 А(2; 2)
А(2; 2)
2) Найдём середину отрезка B 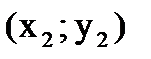
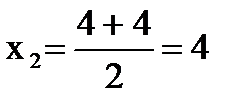
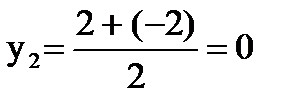
В(4;0)
3) Найдём середину отрезка C(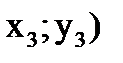
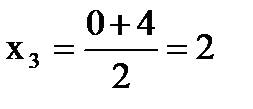
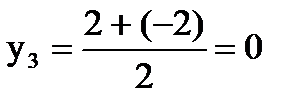
С(2;0)
4) 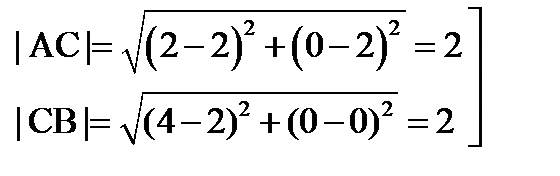
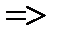 АС=CB
АС=CB 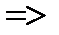 треугольник АВС -равнобедренный, что и требовалось доказать
треугольник АВС -равнобедренный, что и требовалось доказать
б)Дано 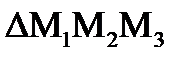 :
:
Доказать, что биссектриса, проведенная из вершины при основании равны.
Доказательство.
1) 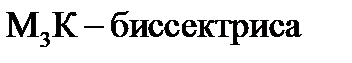
Найдём каноническое уравнение 2-ух точек M3, M1
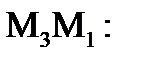
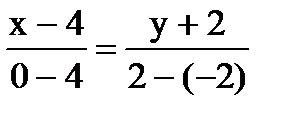
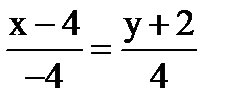
4-x=y+2,
x+y-2=0
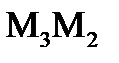 x-4=0
x-4=0
Найдём каноническое уравнение 2-ух точек 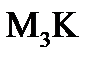
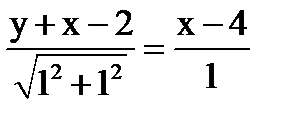
y+x-3= 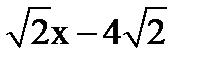
у+(1- 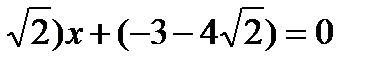
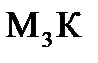
у=2,
y-2=0
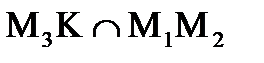 .
.
Составим систему уравнения из 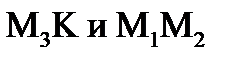
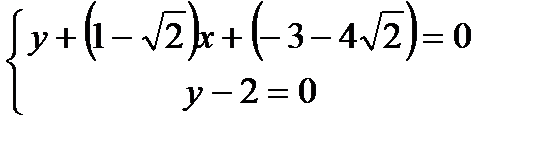
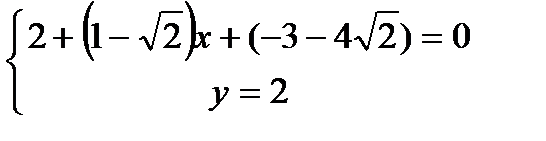
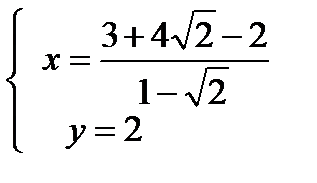
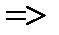 K
K 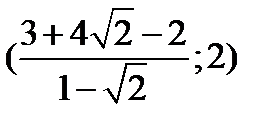
Найдем длину 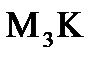 .
.
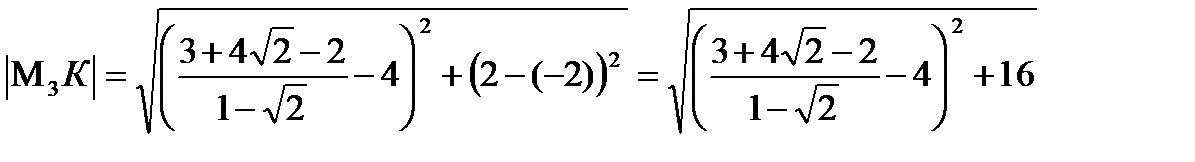
2) Найдём каноническое уравнение 2-ух точек 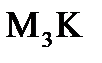
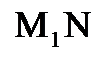
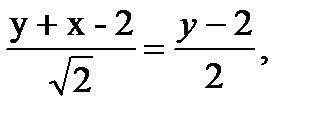
у 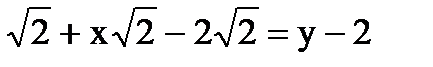
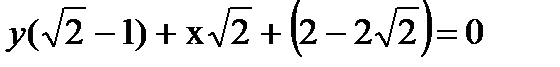
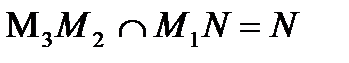
Составим систему уравнения из 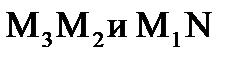
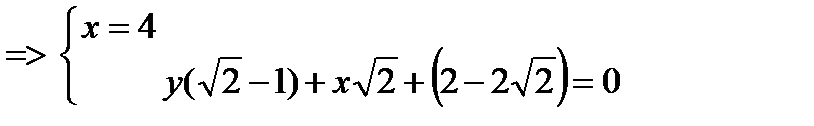
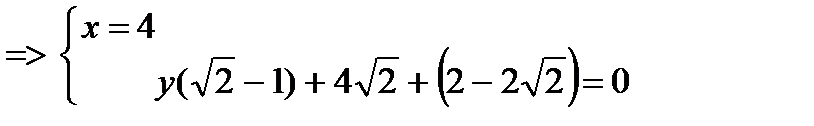
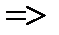
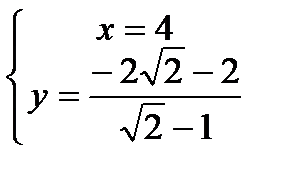
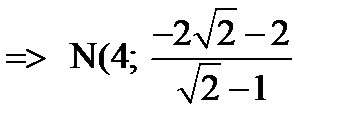
Найдем длину 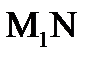
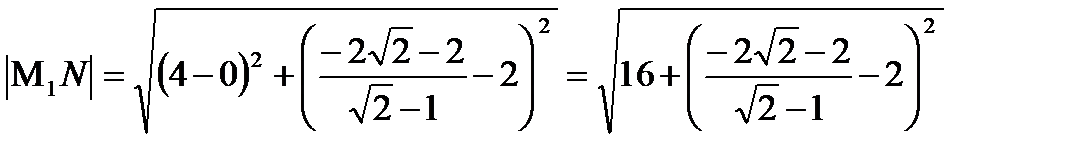
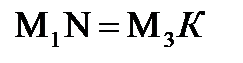 что и требовалось доказать
что и требовалось доказать
в)Дано: ΔАВС и 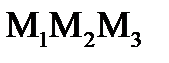 оказать, что медианы, проведенные из вершин при основании равны.
оказать, что медианы, проведенные из вершин при основании равны.
Доказательство.
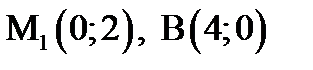
Найдем длину 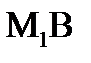
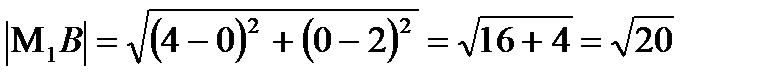
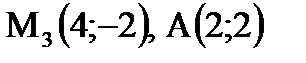
Найдем длину  A
A
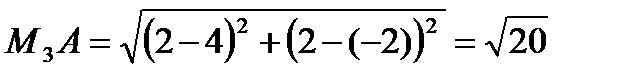
 =
=  A что и требовалось доказать
A что и требовалось доказать
Ответ: а)АС=СВ
б) 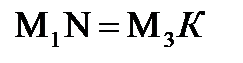
в) 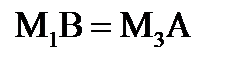
| Дано: Δ АВС; А(0;0), В(3;1), С(1;7). Доказать, что Δ АВС прямоугольный. |
| А |
| В |
| С |
Доказать, что треугольник с вершинами А(0;0), В(3;1), С(1;7) прямоугольный.
Доказательство.
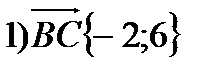
2) 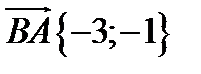
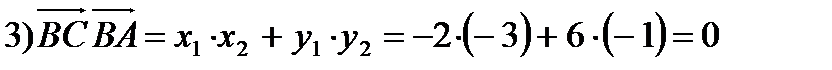 .
.
Скалярное произведение ненулевых векторов равно нулю тогда и только тогда, когда эти вектора перпендикулярны.
Значит <В=90°, следовательно треугольник АВС прямоугольный.
Что и требовалось доказать.
Задача №6.
| Дано: Δ АВС; А(-2;1), В(4;8), С(10;6). Доказать, что Δ АВС тупоугольный. |
| А |
| В |
| С |
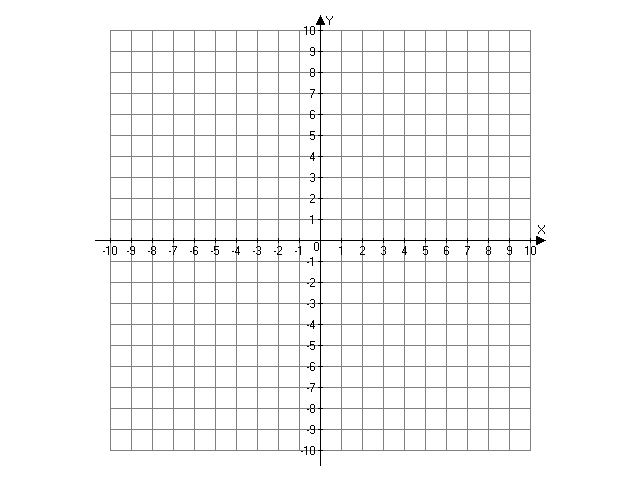
Показать, что в треугольнике А(-2;1), В(4;8), С(10,6) один угол тупой.
Доказательство.
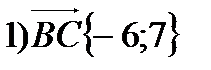
2) 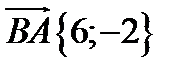
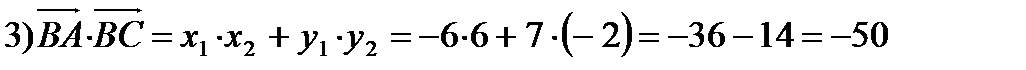 .
.
<B- тупой, так как скалярное произведение двух векторов отрицательно тогда и только тогда, когда между ними тупой угол.
Ответ: Δ АВС тупоугольный.
Дано: ABCD - параллелограмм; А(4;2), В(4;8), С(10;6). DA и СB – диагонали DA  CB=E Найти: а) D. б) CB и DA. в) E. г) CB=E Найти: а) D. б) CB и DA. в) E. г) 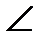 CAB. CAB. |
| В |
| А |
| С |
| D |
| E |
Даны три вершины параллелограмма А(4;2), В(5;7), С(-3;4)
а) Найти координаты четвертой вершины D;
б) Длины диагоналей AD и CB;
в) Точку пересечения диагоналей E;
г) Угол при вершине А.
Решение.
а) Известно, что диагонали параллелограмма в точке пересечения делятся пополам. Поэтому координаты точки E - пересечения диагоналей - найдем как координаты середины отрезка AC. Обозначая их через 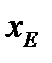 получим, что
получим, что
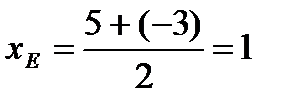 .
.
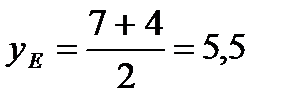
E(1; 5,5)
Зная координаты точки Е – середины диагонали AD и координаты одного из его концов А(4; 2), по формулам
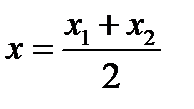
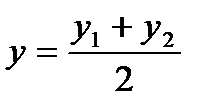
где х=1, 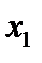 =4, у=5,5,
=4, у=5,5, 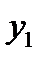 =2, получим
=2, получим
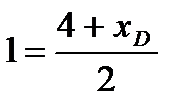 .
.
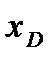 =-2
=-2
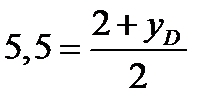
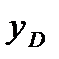 =9
=9
D(-2;9).
б) 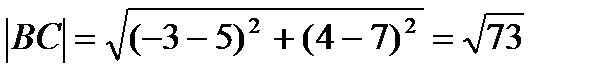
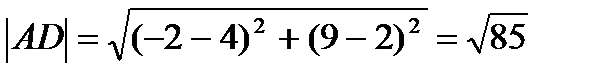
в) Найдем уравнения прямых содержащие диагонали параллелограмма АD и ВС по формуле
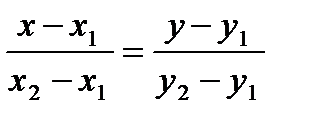 .
.
AD:
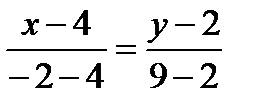 .
.
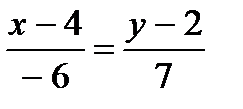
7х-28=-6у+12,
6у+7х-40=0.
ВС:
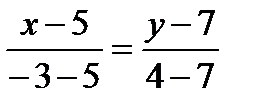
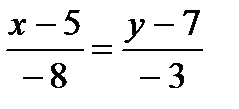
-3х+15=-8у+56,
8у-3х-41=0.
Найдем точку пересечения прямых АD и ВС:
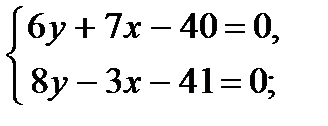 .
.
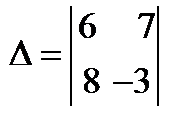 =6(-3)-7
=6(-3)-7  8=-18-56=-74;
8=-18-56=-74;
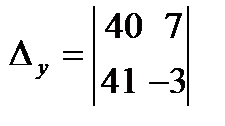 =40
=40 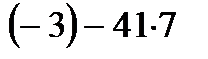 =-120-287=-407;
=-120-287=-407;
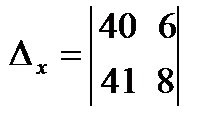 =40
=40 
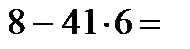 320-246=74;
320-246=74;
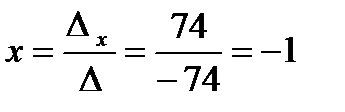 .
.
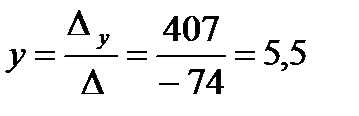
E(-1; 5,5) - точка пересечения диагоналей
г) Найдем уравнение прямых АВ и АС по формуле
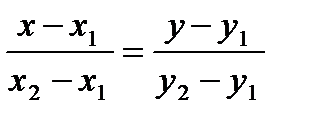 .
.
представим уравнение в виде у=кх+в
АВ:
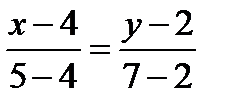
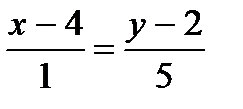
5х-20=у-2,
у=5х-18, 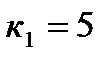 .
.
АС:
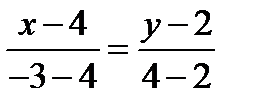
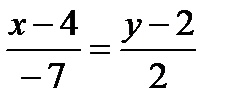
2х-8=-7у+14,
7у=-2х+22,
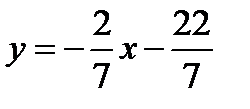 ,
,
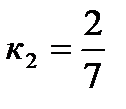 .
.
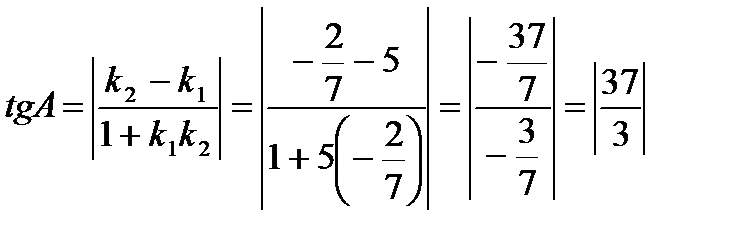
.
<A=arctg 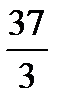
Ответ: а) D(-2;9); б) BC= 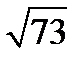 ; АD=
; АD= 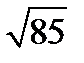 ; в) Е(-1; 5,5); г)
; в) Е(-1; 5,5); г) 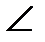 САВ=arctg
САВ=arctg 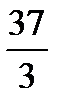
Задача №8.
| В |
| С |
Дано: AB: х+2у=0, BC: х+4у-6=0; AC: х-4у-6=0. Найти 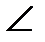 ВAС, ВAС, 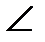 АBС, АBС, 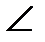 ВCА. ВCА. |
| А |
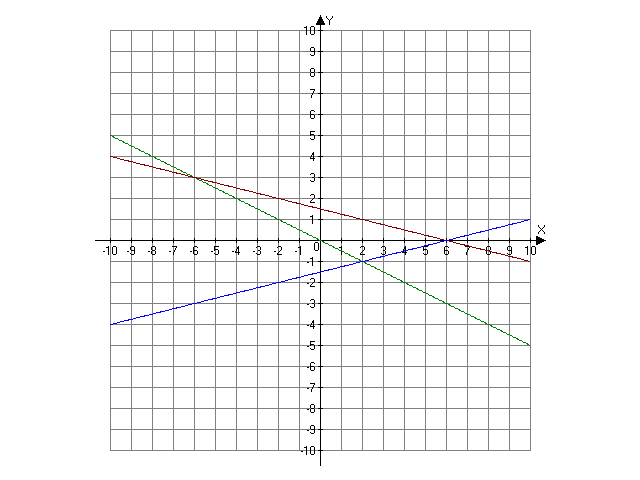
Найти внутренние углы треугольника, стороны которого заданы уравнениями х+2у=0, х+4у-6=0; х-4у-6=0.
Решение
x+2у=0, х+4у-6=0, х-4у-6=0 распишем эти уравнения по формуле у=кх+в
AB:
х+2у=0,
2у=-х,
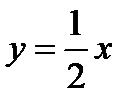 .
.
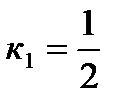
ВС:
х+4у-6=0,
4у=-х+6,
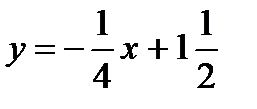 .
.
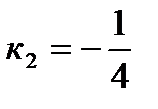
AC:
х-4у-6=0,
4у=х-6,
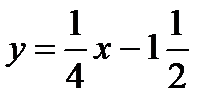
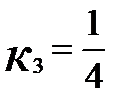
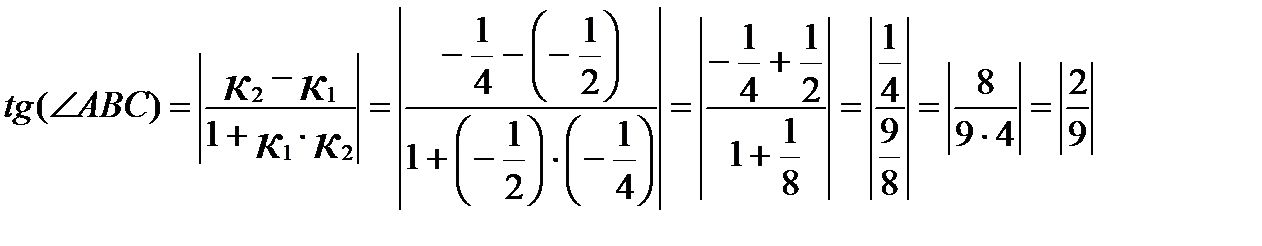
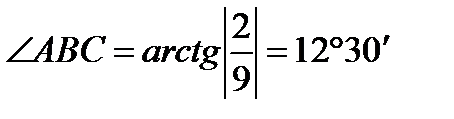
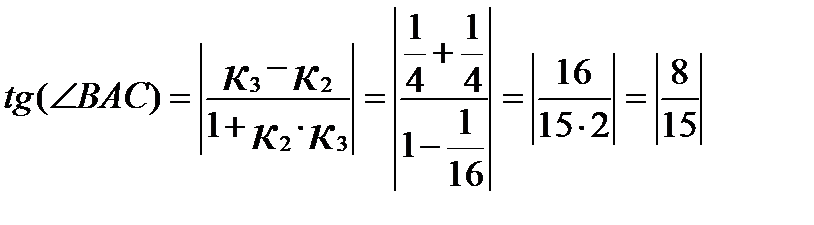
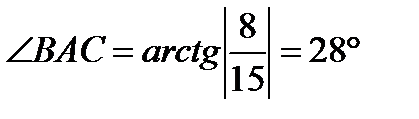
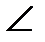 BAC=180°-28°-12°30'=139°30'.
BAC=180°-28°-12°30'=139°30'.
Ответ:  ABC= 12°30';
ABC= 12°30';  BAC=28°;
BAC=28°;  BCA=139°30'.
BCA=139°30'.
Задача №9
Вычислить координаты вершин ромба, если известны уравнения двух его сторон: x+2y=4 и х+2у=10 и уравнение одной из его диагоналей у=х+2
Дано:
Найти: А,В,С и D.
Решение
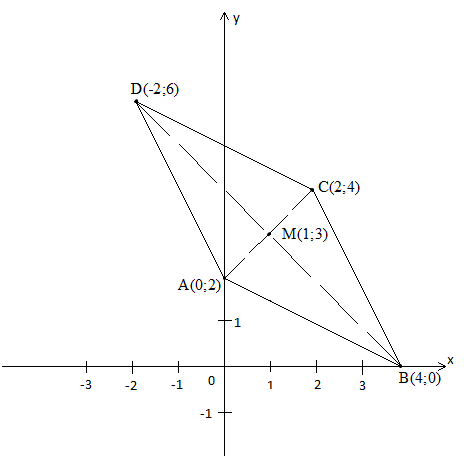
а) Решим 2 системы из 2 линейных уравнений.
1) Первая x+2y=4 и y=x+2 даст одну вершину А ромба:
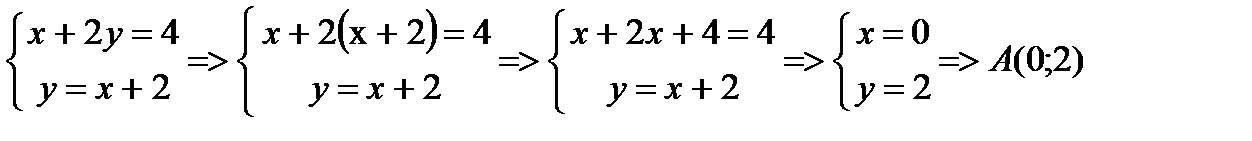 .
.
Вторая х+2у=10 и у=х+2 даст другую вершину С ромба:
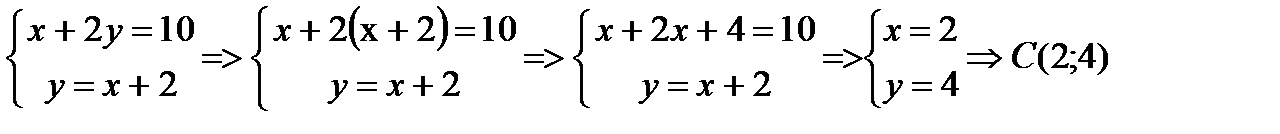 .
.
б) Нашли середину диагонали: (1;3)
в) используя свойство ромба найдем его вторую диагональ (она будет перпендикулярна заданной) у=-x+b, подставим координаты середины отрезка АС - точки М пересечения координат М(1;3) найдем b=4 т.е вторая диагональ
у=-х+b,
b=x+y=1+3=4,
b=4.
y=-x+4.
г) Найдем точки пересечения ее со сторонами — это будут две другие вершины. Решим 2 системы из 2 линейных уравнений.
1) Первая x+2y=4 и y=-x+4 даст одну вершину В ромба:
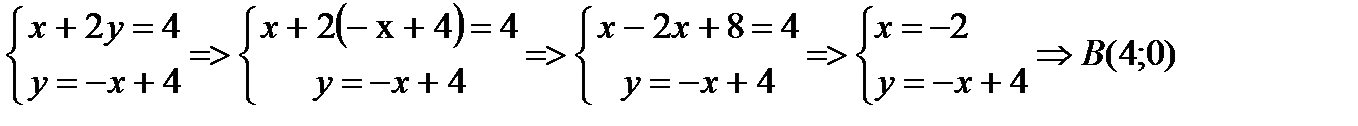
2) Вторая х+2у=10 и у=-х+4 даст другую вершину D ромба:
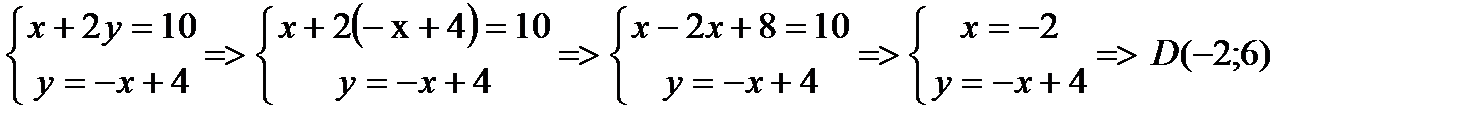
Ответ А(0;2), В(4;0), С(2;4), D(-2;6)
 2015-06-28
2015-06-28 3087
3087