Найти координаты вершин треугольника, если стороны заданы уравнениями:
x - 2y + 3 = 0; 2x - y – 3 = 0; x + y – 3 = 0;
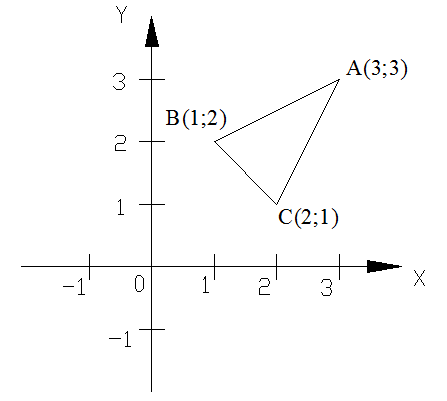
Дано: АВ: х-2у+3=0, АС: 2х-у-3=0, ВС: х+у-3=0
Найти: А,В и С.
Решение.
Найдем вершины треугольника АВС, как точки пересечения сторон треугольника.
т.А:
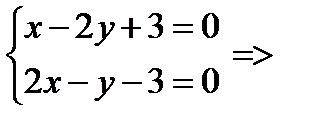
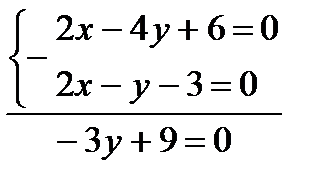
3у=-9 у=3, x-2*3+3=0, у=3, х=3
имеем: A(3;3)
т. В:
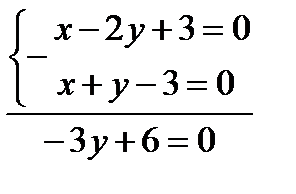 .
.
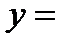 х-2*2+3=0, у=2, х=1
х-2*2+3=0, у=2, х=1
имеем: т. B(1;2)
т.С:
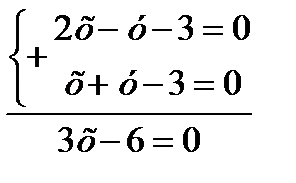 .
.
3х=6 х=2, 2+y-3=0, х=3, y=1
имеем: т. C(2;1)
Ответ: коорд инаты вершин треугольника: А (3;3); В(1;2); С(2;1).
Задача №2
Даны вершины треугольника: 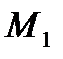 ;2);
;2); 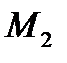 ;3);
;3); 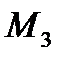 ;1).
;1).
Написать уравнение высоты, опущенной из точки 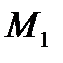
Решение
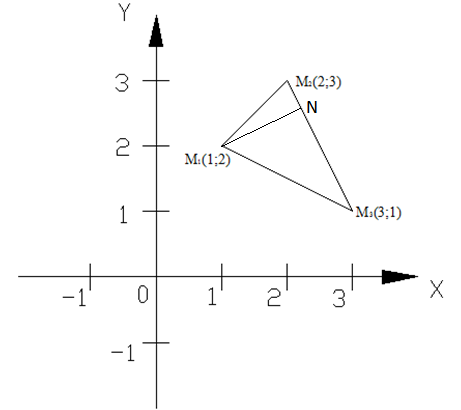
Дано: 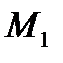 (1;2);
(1;2); 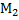 (2;3);
(2;3); 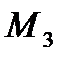 (3;1) - вершины треугольника
(3;1) - вершины треугольника 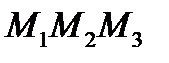
Решение: проведем из точки 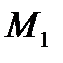 высоту к стороне
высоту к стороне 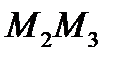 запишем уравнение стороны
запишем уравнение стороны 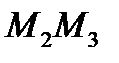
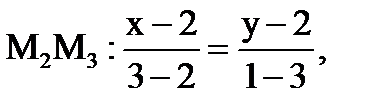
откуда имеем
-2х+4-у+2=0,
у+2х-6=0, у = -2х+6, т.е. угловой коэффициент прямой k= -2. Тогда, угловой коэффициент перпендикулярной прямой (высоты 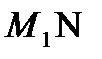 ) будет
) будет 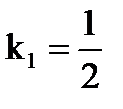 . Найдем уравнение высоты, как уравнение прямой, проходящей через одну точку: y-y1 =k(x-x1), Где x1 и y1 – координаты точки
. Найдем уравнение высоты, как уравнение прямой, проходящей через одну точку: y-y1 =k(x-x1), Где x1 и y1 – координаты точки 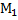 .
.
y-2=  (x-1), откуда имеем 2y-x-3=0
(x-1), откуда имеем 2y-x-3=0
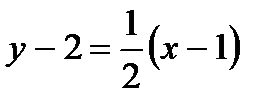 .
.
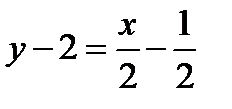 откуда, преобразовав, получим
откуда, преобразовав, получим
2у-х-3=0
Ответ: уравнение высоты 2у-х-3=0
 2015-06-28
2015-06-28 4309
4309