Подобие граничных условий описывается с помощью критерия Нуссельта: 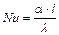 .
.
В данный критерий входит определяемая в задачах по конвективному теплообмену величина 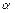 .
.
Условие подобия в ядре потока описывается с помощью критерия Фурье, который характеризует связь между скоростью изменения температурного поля, размерами канала, в котором происходит теплообмен, и физическими свойствами среды в нестационарных условиях: 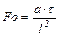 .
.
Критерий Пекле показывает соотношение между количеством тепла, переносимым путем конвекции и теплопроводности при конвективном теплообмене: 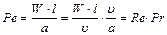 .
.
Критерий Прандтля характеризует поле теплофизических величин потока жидкости: 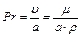 .
.
Критерий Грасгофа вводится при теплообмене в условиях естественной конвекции и показывает меру отношения сил трения к подъемной силе, определяемой разностью плотностей в различных точках потока:
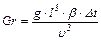 ,
,
где β –коэффициент объемного расширения жидкости, К-1;
∆t – разность температур горячих и холодных частиц жидкости, вызывающих естественную конвекцию, К.
Необходимыми условиями подобия переноса тепла является соблюдение гидродинамического и геометрического подобия. Первое характеризуется равенством критериев Re в сходственных точках подобных потоков, второе - постоянством отношения основных геометрических размеров стенки L1, L2, …,Ln к некоторому характерному размеру.
Таким образом, с учетом того, что критерий Nu является определяемым, т.к. в него входит искомая величина коэффициента теплоотдачи α, критериальное уравнение конвективного теплообмена выражается в виде:
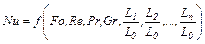 . (1.6)
. (1.6)
Вид функции (1.6) определяется опытным путем, причем обычно ей придают степенную форму. Например, при движении потока в трубе диаметром d идлиной l уравнение (1.6) примет вид:
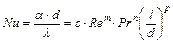 , (1.7)
, (1.7)
где величины с, т, п, р определяются по опытным данным.
Коэффициент теплоотдачи 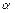 определяется по найденному из критериальных уравнений критерию Нуссельта.
определяется по найденному из критериальных уравнений критерию Нуссельта.
 2015-06-28
2015-06-28 583
583








