2015-06-28
571
«Поиск решения»
1) Ввод данных. Переносим данные задачи в EXCEL. Результаты заполнения таблицы EXCEL можно увидеть на рис.24:
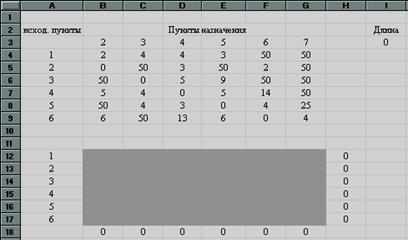
Рис.24
В ячейках B4: G9 введены длины путей из исходных пунктов в пункты назначения.
Ячейки B12: G17 являются изменяемыми ячейками для нашей процедуры.
В ячейках B18: G18 находятся суммы значений соответствующих столбцов изменяемых ячеек. Так в ячейке B18 находится сумма ячеек B12: B17. Аналогично в ячейках:
в С18 находится сумма ячеек С12: С17;
в D18 находится сумма ячеек D12: D17;
в E18 находится сумма ячеек E12: E17;
в F18 находится сумма ячеек F12: F17;
в G18 находится сумма ячеек G12: G17.
В ячейках H12: H17 находятся суммы значений соответствующих строк изменяемых ячеек. Так в ячейке H12 находится сумма ячеек B12: G12. Аналогично в ячейках:
в H13 находится сумма ячеек B13: G13;
в H14 находится сумма ячеек B14: G14;
в H15 находится сумма ячеек B15: G15;
в H16 находится сумма ячеек B16: G16;
в H17 находится сумма ячеек B17: G17.
Целевая функция заносится в ячейку I3 и вычисляется по формуле «СУММПРОИЗВ (B4:G9; B12:G17)».
2) Заполнение окна процедуры «Поиск решения».
целевая функция: I3;
значение целевой функции: min;
изменяемые ячейки: B12: G17;
ограничения задачи:
B18: G18 = 1 и H12: H17 = 1;
B12: G17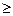 
0 (ячейки должны иметь положительные значения).
В окне «Параметры» установить «Линейная модель», что соответствует решению задачи симплекс-методом. Результаты заполнения окна показаны на рис.25:
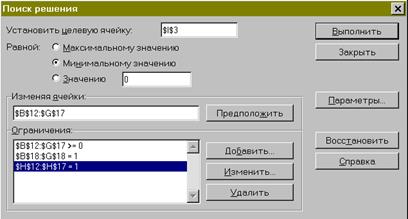
Рис.25
3) Выполнив процедуру «Поиск решения» в первоначальной таблице (рис. 24) получим следующие результаты (рис.26):
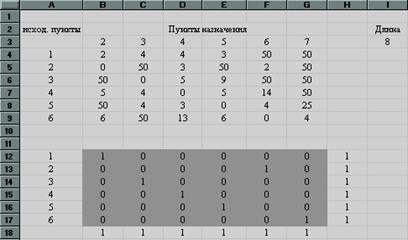
Рис. 26
Эти результаты определяют следующее решение задачи:
1 ® 2 ® 6 ® 7, длина пути = 8.
