Основные определения. 1. Линейной комбинацией векторов называют вектор

1. Линейной комбинацией векторов 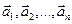называют вектор

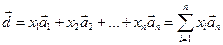, (7.7)

где 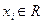(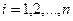) – коэффициенты линейной комбинации.

2. Система n векторов 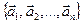называется линейно зависимой, если существуют числа 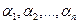, не равные нулю одновременно, что выполняется равенство

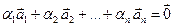. (7.9)

3. Коэффициенты а_x, а_y, а_z разложения вектора 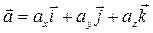по базисным ортам 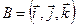называются координатами вектора в данном базисе

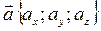. (7.10)

16. Задача 1 (Элементы векторной алгебры. С.7)

17. Задача 2 (ЭВА. С.7)

18. В треугольнике АВС сторона АВ точками M и N разделена на части: АМ=MN=NB. Найдите вектор 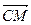, если , .

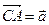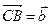19. В треугольнике АВС сторона АМ – биссектрисаугла ВАС, причем точка М лежит на стороне ВС. Найдите вектор 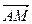, если , .

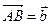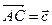20. Пример 7 (ЭВА. С.9)

21. Пример 9 (ЭВА. С.11)

22. Пример 8 (ЭВА. С.10)

23. Найдите линейную комбинацию векторов 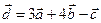, где , , .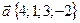

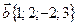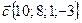24. Вычислите координаты линейной комбинации векторов 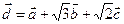, где , , .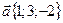

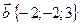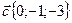25. Вычислите координаты вектора 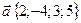в базис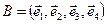е , где , , ,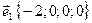

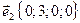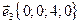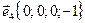
26. Выясните, является ли система векторов линейно независимой , , .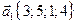

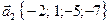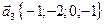27. Выясните, является ли система векторов линейно независимой , , .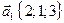

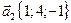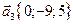28. Даны векторы 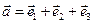, , 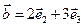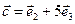в базисе 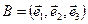. Докажите, что векторы 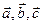образуют базис. Вычислите координаты вектора 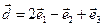в базисе .

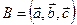29. Выясните, раскладывается ли вектор 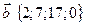через векторы системы: , , .

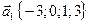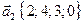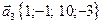30. Выясните, раскладывается ли вектор 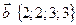через векторы системы: , , .

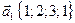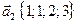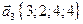Д/з: 1) Повторите теорему о коллинеарных векторах, теорему о компланарных векторах,

2) выполните оставшиеся номера