Примеры

Векторы и действия над ними

…………...

Скалярное произведение векторов

1. Скалярным произведением векторов

= (a ₁, a ₂, …, a_n) и = (b ₁, b ₂, …, b_n) называется число,

(, ) = × = a ₁× b ₁ + a ₂× b ₂ + … + a_n × b_n.

Свойства скалярного произведения векторов:

(, ) = (, );

( + , ) = (, ) + (, );

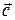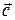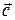(k ₁ , k ₂ ) = k ₁ k ₂(, ).

Длина вектора :

.

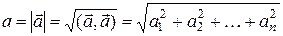Расстояние между точками А (a ₁, a ₂, …, a_n) и

В (b ₁, b ₂, …, b_n) определяется как длина вектора :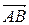

.

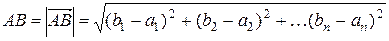Углом между векторами и называется угол ,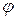

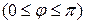косинус которого определяется равенством:

.

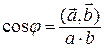Для скалярного произведения векторов справедливо равенство:

.

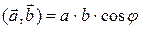Векторы и называются ортогональными

(перпендикулярными), если .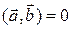

Примеры.

2. Векторное произведение векторов (в R³)

1. Векторным произведением векторов 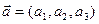и

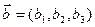будем называть вектор 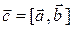который

получен по правилу определителя:

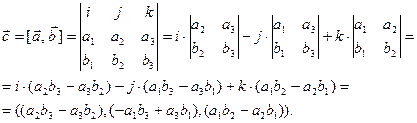
Геометрическое определение векторного произведения.

Векторным произведением векторов и называется

такой вектор 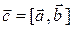который:

а) перпендикулярен каждому из векторов и ;

б) направлен так, что если смотреть с его конца, то

поворот первого вектора (т. е. вектора ) ко второму

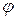(т. е. к вектору ) на кратчайший угол проходит

против часовой стрелки;

в) длина вектора 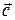равна произведению длин векторов и

на синус угла между ними, т. е. .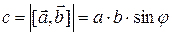

Для векторного произведения векторов и используется

также обозначение .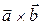

2. Основные свойства векторного произведения векторов:

а) ,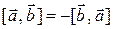

б) ,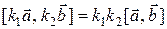

в) ,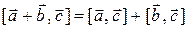

г) если векторы и коллинеарны,

то 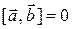. В частности, .

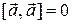3. Если векторы и заданы в координатной форме:

= (a ₁, a ₂, a ₃), = (b ₁, b ₂, b ₃), то

.

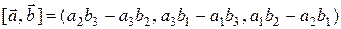Для вычисления векторного произведения векторов удобно пользоваться следующей таблицей:

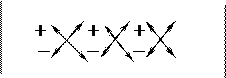
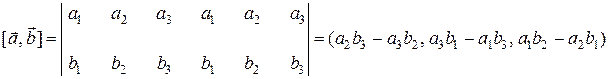
4. Площадь параллелограмма S_{парал .}, построенного на

векторах и численно равна длине вектора :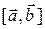

.

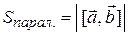5. Площадь треугольника S_треуг., построенного на

векторах и :

.

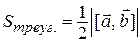Примеры.

3. Смешанное произведение векторов (в R³)

1. Смешанным произведением векторов , и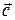

называется число, обозначаемое 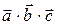и

определяемое формулой:

.

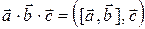2. Объем параллелепипеда (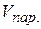), построенного на

векторах , и 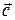определяется формулой: .

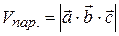3. Объем пирамиды 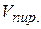, построенной на векторах , и :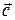

.

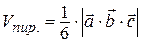4. Условие компланарности векторов , и :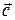

.

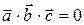Векторы называются компланарными, если они лежат в одной плоскости.