Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними, т.е. 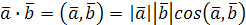
Из определения следует 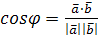 где
где 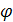 – угол между векторами
– угол между векторами 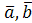 .
.
Свойства скалярного произведения:
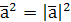 - скалярный квадрат.
- скалярный квадрат.
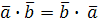 .
.
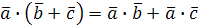 .
.
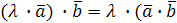 ).
).
Приложения скалярного произведения:
Определение косинуса угла между векторами:
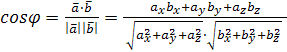 .
.
Нахождение проекции вектора на заданное направление:
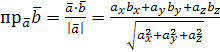 ,
, 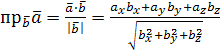 .
.
Пример. Найти косинус угла 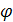 между векторами
между векторами 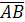 и
и 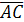 , если
, если 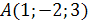 ,
, 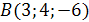 ,
, 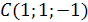 .
.
Решение. Найдем координаты векторов 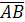 и
и 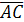 и их модули:
и их модули:
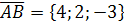 ,
, 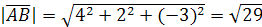 .
.
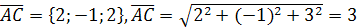 .
.
Определение. Векторным произведением вектора 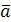 на вектор
на вектор 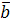 называется третий вектор
называется третий вектор 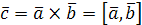 определяемый следующим образом:
определяемый следующим образом:
длина его равна площади параллелограмма, построенного на векторах 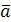 и и 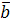 , т.е. , т.е. 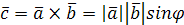 , где , где 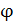 – угол между векторами – угол между векторами 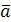 и и 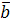 ; вектор ; вектор 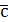 перпендикулярен векторам перпендикулярен векторам 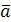 и и 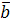 ; векторы ; векторы 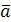 , , 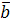 , , 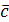 после приведения к общему началу образуют правую тройку векторов. Свойства векторного произведения после приведения к общему началу образуют правую тройку векторов. Свойства векторного произведения 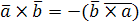 . . 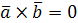 , если или , если или 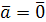 , , 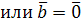 , или , или 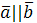 условие коллинеарности векторов. 3. условие коллинеарности векторов. 3. 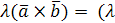 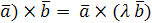 . . | 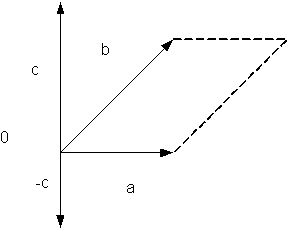 |
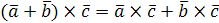 .
.
Приложения векторного произведения:
Установление коллинеарности векторов: (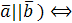 (
(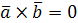 ), т.е.
), т.е.
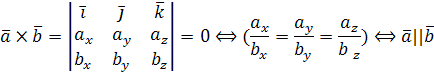
Нахождение площади параллелограмма и треугольника:
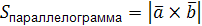 ,
, 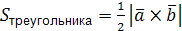
Пример. Вычислить площадь треугольника с вершинами 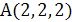 ,
, 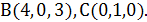
Решение. Найдем координаты векторов
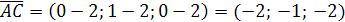 ;
;
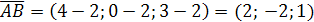 .
.
Вычислим векторное произведение
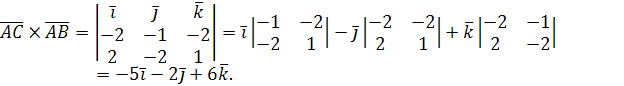
Найдем модуль вектора 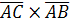 ,
,
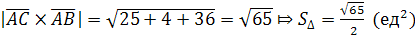 .
.
Определение. Смешанным произведением трех векторов 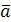 ,
, 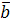 ,
, 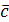 называется число
называется число 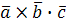 .
.
Геометрический смысл смешанного произведения: модуль смешанного произведения трех векторов численно равен объему параллелепипеда, построенного на этих векторах.
Пусть ребрами параллелограмма являются векторы 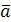 ,
, 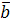 ,
, 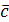 образующие правую тройку векторов и вектор
образующие правую тройку векторов и вектор 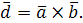
Имеем 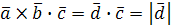 ?
? 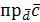 , так как
, так как 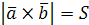 – площадь основания построенного на векторах
– площадь основания построенного на векторах 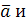
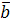 , а
, а 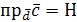 – высота параллелограмма, то
– высота параллелограмма, то 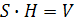 – объем параллелограмма построенного на правой тройке векторов
– объем параллелограмма построенного на правой тройке векторов  ,
, 
 .
.
Для левой тройки векторов 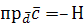 .
.
Получаем, 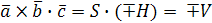 , где
, где 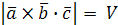 – объем параллелепипеда построенного на векторах
– объем параллелепипеда построенного на векторах 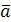 ,
, 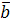 ,
, 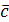 .
.
 2015-01-13
2015-01-13 29197
29197
