Если А - квадратная матрица порядка n, то любой ненулевой вектор размера 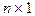 (матрица - столбец размера
(матрица - столбец размера 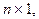 для которого справедливо матричное уравнение
для которого справедливо матричное уравнение
(6) 
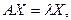
где 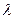 - некоторое число, называется собственным вектором матрицы А, а
- некоторое число, называется собственным вектором матрицы А, а
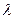 - принадлежащим ему собственным значением матрицы А.
- принадлежащим ему собственным значением матрицы А.
Матричное уравнение (6) эквивалентно линейной системе
(6¢) 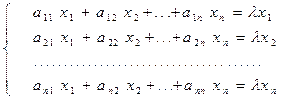
Перенесем члены, стоящие в правых частях уравнений, в их левые части и приведем подобные члены. Получим однородную систему уравнений:
(7¢) 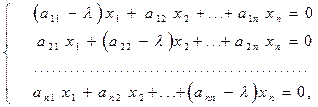
которая в свою очередь эквивалентна матричному уравнению:
(7) 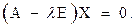
Т.к. по определению собственный вектор (столбец неизвестных данной системы) является ненулевым вектором, нам нужны нетривиальные решения системы ( , следовательно, определитель последней системы должен быть равен нулю, т.е.
, следовательно, определитель последней системы должен быть равен нулю, т.е.
(8) 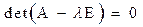 .
.
Последний определитель получается из элементов исходной матрицы А вычитанием собственных значений 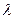 из ее диагональных элементов:
из ее диагональных элементов:
(8¢) 
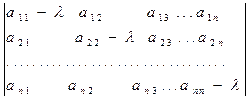 =0.
=0.
Вычисляя определитель, мы получим некоторый многочлен n -й степени относительно 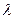 . Данный многочлен
. Данный многочлен 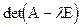 называется характеристическим многочленом матрицы А, а уравнение (8) - характеристическим уравнением ее. Решениями характеристического уравнения являются собственные значения
называется характеристическим многочленом матрицы А, а уравнение (8) - характеристическим уравнением ее. Решениями характеристического уравнения являются собственные значения 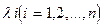 матрицы А.
матрицы А.
Представляя каждое из найденных значений 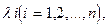 в уравнение (7) и находя нетривиальное решение его
в уравнение (7) и находя нетривиальное решение его  , мы находим собственный вектор матрицы А, принадлежащий собственному значению
, мы находим собственный вектор матрицы А, принадлежащий собственному значению 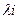 .
.
Пример 7. Найти собственные значения и собственные векторы матрицы А, где 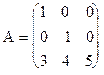 .
.
Составим характеристическое уравнение матрицы А:
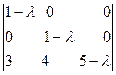 = 0.
= 0.
Раскроем определитель по правилу треугольника:
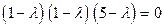 .
.
После перемножения скобок и приведения подобных членов, будем иметь уравнение 3-й степени (матрица А 3-го порядка) относительно 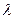 ; но удобнее. не выполняя этих преобразований, каждый множитель приравнять нулю, тем самым мы находим собственные значения матрицы А:
; но удобнее. не выполняя этих преобразований, каждый множитель приравнять нулю, тем самым мы находим собственные значения матрицы А:
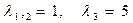 .
.
Берем первое из них и составляем систему 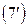 для нахождения собственного вектора, соответствующего ему:
для нахождения собственного вектора, соответствующего ему:
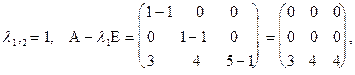 т.е.
т.е.
имеем уравнение: 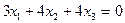 или
или 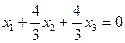 . Откуда имеем
. Откуда имеем
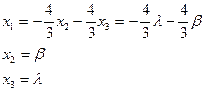
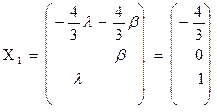
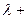
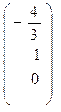
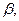 где
где 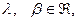
т.е. собственному значению 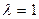 соответствует два линейно независимых собственных вектора:
соответствует два линейно независимых собственных вектора:
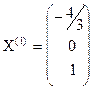 и
и 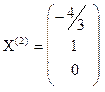 или
или 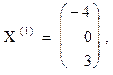
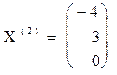
Берем следующее собственное значение 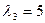 и составляем систему для нахождения соответствующего ему собственного вектора:
и составляем систему для нахождения соответствующего ему собственного вектора:
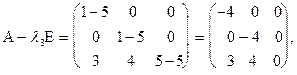 т.е.
т.е. 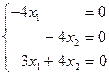
Т.к. 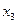 в этой системе не содержится, придаем ему произвольные значения
в этой системе не содержится, придаем ему произвольные значения
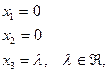
Т.е. собственному значению 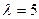 соответствует собственный вектор
соответствует собственный вектор
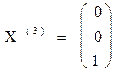
 .
.
 2015-06-28
2015-06-28 294
294






