Геометрична прогресія

Формули скороченого множення

(а−в)(а+в) = а²−в²

(а+в)² = а²+2ав+в²

(а−в)² = а²−2ав+в²

(а+в)³ = а³+3а²в+3ав²+в³

(а−в)³ = а³−3а²в+3ав²−в³

Розкладання на множники

а²−в² =(а−в)(а+в)

а³+в³ = (а+в)(а²−ав+в²)

а³−в³ = (а−в)(а²+ав+в²)

ах²+вх+с = а(х−х₁)(х−х₂)

Формула коренів квадр. рівняння ах²+вх+с = 0

D = в² − 4ас

х_1,2 =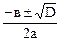

Теорема Вієта

х² + рх + q = 0

х₁ + х₂ = − р

х₁х₂ = q

Координати вершини параболи

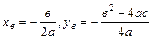
Властивості квадратних коренів

;

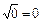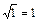
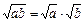
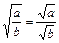
	n = 3	n = 4	n = 6
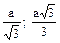
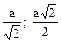
R			a
r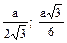
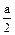
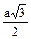
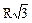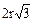
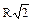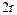
а	;	;	R;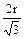

;

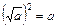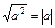
Властивості степенів

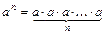
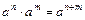
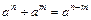
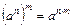
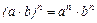
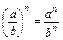
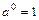
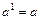
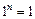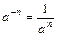
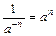
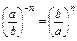
Арифметична прогресія

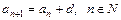
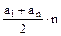d = a2−a1 an = a1+ (n−1)∙d Sn = Sn=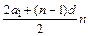

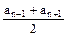d = an+1−an an = ak+ (n−k)∙d an = an =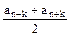

Геометрична прогресія

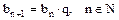
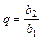
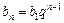
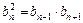
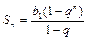
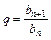
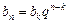
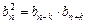
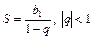−	сума нескінченої геом. прогр.

В правильному n–кутнику:

Сума всіх кутів: 180°· (n – 2)

Внутрішній кут: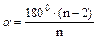

Зовнішній кут: 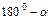або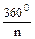

Центральний кут: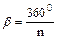

Сторона: 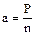, де Р – периметр

Апофема: радіус вписаного кола r

Радіуси опис. і впис. кола:
Довільний трикутник

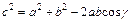
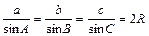
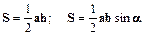
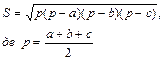
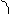
b α h с

а

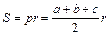
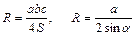
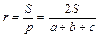
Медіани трикутника перетинаються в одній точці і точкою перетину діля- ться у відношені 2:1 починаючи від вершини. В

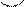
Властивість бісектриси:

AB:AD = BC:CD

AB:BC = AD:CD A D C