Основные понятия по теме. Система булевых функций называется полной, если любую булеву функцию можно представить в виде суперпозиции функций из

Система булевых функций 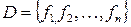называется полной, если любую булеву функцию можно представить в виде суперпозиции функций из .

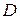Например, следующие системы 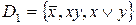, , 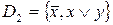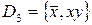являются полными.

Множество 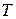булевых функций называется замкнутым классом, если любая суперпозиция функций из 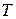снова принадлежит .

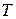Всякая система 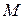булевых функций порождает некоторый замкнутый класс. Этот класс состоит из всех булевых функций, которые можно получить суперпозициями из 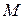. Такой класс называется замыканием 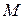и обозначается 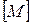. Для замкнутого класса 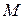следует, что 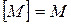. Очевидно, что если 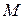- полная система, то .

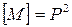Рассмотрим следующие классы булевых функций.

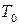- класс булевых функций, сохраняющих константу 0, т.е. функций 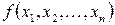, для которых .

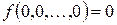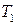- класс булевых функций, сохраняющих константу 1, т.е. функций 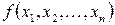, для которых .

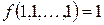Булева функция 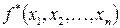называется двойственной к функции 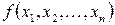, если .

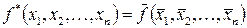Булева функция 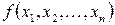называется самодвойственной, если она совпадает с двойственной, т.е. .

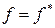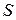– класс всех самодвойственных функций.

Булевы функции вида 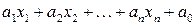, где 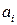, 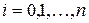равны нулю или единице, называются линейными.

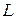– класс всех линейных булевых функций.

Для того, чтобы определить, является ли данная булева функция линейной или нет, ее надо представить в виде полинома Жегалкина.

Два набора 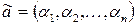и 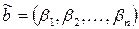называются сравнимыми, если , .

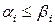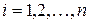Запись 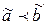означает, что набор 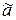предшествует набору .

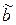Булева функция 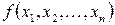называется монотонной, если для любых наборов 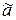и 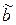таких, что 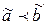, имеет место неравенство .

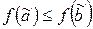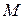– класс монотонных функций.

Теорема (о функциональной полноте) Для того, чтобы система булевых функций была полной, необходимо и достаточно, чтобы она целиком не содержалась ни в одном из пяти классов , , , , .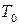

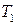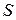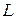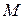В тех задачах, где требуется выяснить, является ли данная система булевых функций 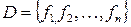полной, мы будем составлять таблицы, которые называются таблицами Поста.

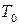
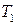
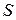
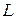
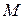
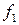
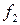
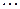
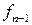
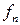
В клетках данной таблицы мы будем писать плюс или минус, в зависимости от того, входит функция, стоящая в данной строке в класс, стоящий в данном столбце, или не входит. Используя теорему о полноте, мы получаем, что для полноты данной системы булевых функций необходимо и достаточно, чтобы в каждом столбце стоял хотя бы один минус.

Пример 1 Выяснить, является ли функция 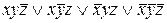линейной.

Найдем полином Жегалкина для данной функции.

,

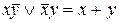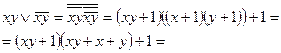
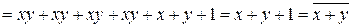
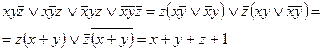
Следовательно, данная функция линейна.

Пример 2 Какие из указанных функций являются монотонными:

а) 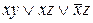б)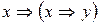

а) Упростим формулу 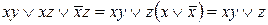. Эта функция равна нулю на наборах (0,0,0), (0,1,0), (1,0,0). Все оставшиеся наборы, исключая (0,0,1) содержат не менее двух единиц, а значит, они могут быть только больше. Набор (0,0,1) 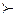(0,0,0), а с остальными двумя он несравним. Значит, рассматриваемая функция монотонна.

б) Функция немонотонна, т.к. (0,0) 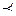(1,0), но

.

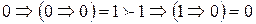Пример 3 Является ли функция 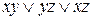самодвойственной?

Найдем двойственную функцию к данной

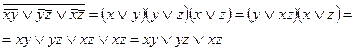
Следовательно, данная функция самодвойственная.

Пример 4 Выяснить, являются ли данные системы булевых функций полными

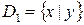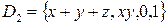а) ; б) ; в)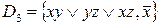

а) 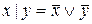. Ясно, что 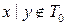, 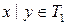. Так как 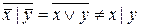, то 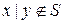. Найдем полином Жегалкина для 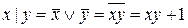. Следовательно, 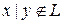. Так как (0,0) 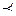(1,1), н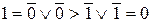о , то 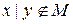. Таблица Поста для системы 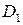имеет вид.

	–	–	–	–	–

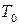
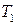
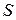
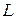
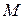
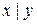
Итак, 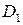- полная система.

б)

	+	–	–	+	+
	–	+	–	+	+
	+	+	–	–	+
	+	+	+	+	–

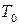
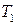
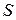
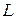
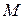
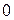
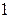
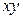
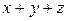
Функция 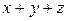самодвойственная, так как

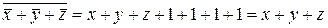
Функция 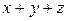немонотонная, так как (0,0,1) 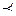(0,1,1), но 1=0+0+1>0+1+1=0.

Система 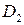- полная система.

в)

	–	–	+	+	–
	+	+	+	–	–

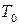
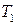
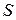
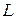
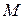
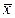
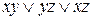
Функция 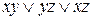самодвойственная, так как

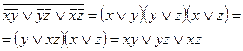
Итак, система 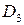целиком принадлежит классу 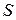. Следовательно, по теореме о полноте 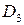не является полной системой.