Рассмотренные ранее такие понятия как цикломатическое число и ранг, являются одними из важных числовых характеристик графов. Они определяют, соответственно, количество базисных циклов и базисных разрежающих множеств следующим образом:
1. Количество базисных циклов графа G равно цикломатическому числу графа - числу ребер в кодереве.
2. Количество базисных разрежающих множеств равно величине ранга графа - числу ребер в остове.
Построим цикломатическую матрицу C = (cik) и матрицу разрезов S = (sjk) графа, элементы которых:
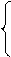
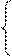 1, если gk Î Ci; 1, если gk Î Sj;
1, если gk Î Ci; 1, если gk Î Sj;
cik = sjk =
0, если gk Ï Ci. 0, если gk Ï Sj.
Каждая строка матриц C и S определяет некоторый цикл и разрез графа. Количество строк этих матриц равно числу всех циклов и разрезов исходного графа G соответственно. Эти строки матриц, а также соответствующие им циклы и разрезы, можно получить как суперпозицию базисных циклов и разрежающих множеств.
Суперпозиция осуществляется с помощью операции сложения по модулю 2 двоичной алгебры, обозначаемой символом Å. Вектор-строка сi = (ci1, ci2, …, cim), описывающая цикл Ci графа, вычисляется как покомпонентная сумма по модулю 2 векторов, соответствующих базисным циклам. Аналогично, вектор-строка sj = (sj1, sj2, …, sjm) описывает разрез Sj графа и вычисляется как сумма по модулю 2 векторов, соответствующих базисным разрезающим множествам.
Рассмотрим пример построения этих матриц для графа, приведенного на рис. 3.30. Сначала вычислим ранг и цикломатическое число этого. Ранг графа – число ребер в остове (рис. 3.31) – равен 4. Цикломатическое число графа – число ребер в кодереве (рис. 3.32) – равно 3. Следовательно, имеем 3 базисных цикла и 4 базисных разрезающих множества. Далее запишем эти базисные циклы и разрезающие множества.
Базисные циклы:
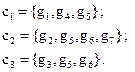
Базисные разрезающие множества:
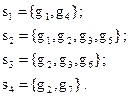
 2015-06-28
2015-06-28 473
473








