Основна
1. Новоселов В.Г., Скатков А.В. Прикладная математика для инженеров-системотехников. Дискретная математика в задачах и примерах. – К.: Учебно-методический кабинет высшего образования, 1992. - С.137-148.
2. Новиков Ф.А. Дискретная математика для программистов. – СПб.: Питер, 2001. - С.94-98.
3. Горбатов В.А. Основы дискретной математики. – М.: Высш.шк., 1986. - С.55-73.
Додаткова
4. Яблонский С.В. Введение в дискретную математику. – М.: Наука, 1979. - С.23-35.
5. Сигорский В.П. Математический аппарат инженера. – К.: Техника, 1975. - С.504-522.
Для практичних занять
6. Методичні вказівки і завдання до контрольних робіт з дисципліни «Основи дискретної математики» для студентів очної та заочної форм навчання фахів 6.0804, 6.0915 / О.М. Мартинюк. – Одеса: ОНПУ, 2001. – С.30-35.
7. Гаврилов Г.П., Сапоженко А.А. Сборник задач по дискретной математике. – М.: Наука, 1973. - С.50-77.
Лекція 26. Графічна та таблична мінімізація
Вступ
Лекція має за мету навести два найбільш наочних метода мінімізації булевих функцій. Розглянута відповідність між мінтермами (макстермами) та елементами n-вимірного куба, а також мінтермами та клітками таблиці Карно і Закревського. Звернено увагу до кодування стовпців та рядків карт Карно і Венна, до обмежень графічного і табличного методів.
У лекції присутні два підрозділи:
26.1. Графічний метод мінімізації булевих функцій
26.2. Табличний метод мінімізації
26.1. Графічний метод мінімізації булевих функцій
Кожній вершині n-мірного куба можна поставити у відповідність константу одиниці. Отже, підмножина відзначених вершин є відображенням булевої функції від n змінних у СДНФ.
Для відображення функції від n змінних, представленої в СДНФ, необхідно установити відповідність між її мінтермами й елементами n-вимірного куба.
Мінтерм n-го рангу для функції n-змінних відповідає вершині
n-вимірного куба. Мінтерм (n-1)-го рангу можна розглядати як результат доповнення двох мінтермів n-го рангу, що відрізняються однією змінною:
jn-1=(jn-1×xi)Ú(jn-1×`xi).
На n-вимірному кубі це відповідає заміні двох вершин, що відрізняються значенням одної змінної, ребром, що з'єднує ці вершини. Говорять, що ребро покриває інцидентні йому вершини. Таким чином, мінтермам (n-1)-го порядку відповідають ребра n-вимірного куба.
Аналогічно установлюється відповідність мінтермів (n-2)-го порядку граням n-вимірного куба, кожна з яких покриває чотири вершини або два ребра (квадрат).
Елементи n-вимірного куба, що характеризуються ²S² вимірами, називаються s-кубами. Так вершини називаються 0-кубами, ребра -
1-кубами, грані - 2-кубами і т.д. Таким чином, будь-яка ДНФ відображається на n-вимірному кубі сукупністю S-кубів, що покривають усі відзначені вершини, які відповідають конституентам «1» (0-кубам). Говорять, що така сукупність S-кубів чи мінтермів утворить покриття функції.
Приклад. Для функції від трьох змінних y= x1`x2`x3 Ú x1`x2 x3 Ú Ú`x1`x2 x3 Ú`x1 x2 x3 Ú`x1 x2`x3 Ú x1 x2 x3, заданої у вигляді СДНФ, графічний метод дає формулу вигляду ymin= x3Ú`x1x2Ú
Ú x1`x2 = x3 Ú (x1 Å x2).
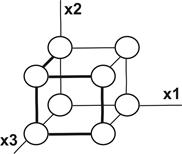
Рис. 26.1. Грань і ребра для функції ymin = x3 Ú`x1 x2 Ú x1`x2
у графічному методі мінімізації
Мінімізація на n-вимірному кубі зводиться до пошуку такого покриття, число S-кубів якого буде мінімально, а їхня розмірність S максимальна. Таке покриття називають мінімальним покриттям, а відповідна йому ДНФ - мінімальною ДНФ (МДНФ).
Аналогічно можна виконати мінімізацію графічним способом для КНФ, для цього необхідно замість СДНФ і мінтермів розглядати СКНФ і макстерми.
Даний метод наочний і простий при n=3. При n³4 метод складний.
26.2. Табличний метод мінімізації
Частіше за все у табличному методі використовуються карти Карно - спеціальним чином організовані таблиці відповідності: стовпці і рядки таблиці відповідають усілякім наборам не більше двох змінних, причому ці набори розташовані в такому порядку, що кожен наступний відрізняється від попереднього значенням тільки однієї з змінних. ЗавдЯкі цьому сусідні по вертикалі і горизонталі клітки відрізняються тільки однією змінною. Клітки, розташовані симетрично по краях таблиці також вважаються сусідніми і відрізняються однією змінною. Карта Карно представляє функцію у так званому коді Грея.
Для ДНФ клітки наборів, на яких функція приймає значення «1» заповнюються «1». Нульові клітки не заповнюються. Для КНФ клітки наборів, на яких функція приймає значення «0» заповнюються «0». Одиничні клітки не заповнюються.
Аналогічно n-вимірному кубу, сукупності двох сусідніх кліток відповідає 1-куб, 4-х сусідніх кліток - 2-куб і т.д.
Зчитування мінтермів здійснюється за таким правилом: клітки, що утворюють S-куб дають мінтерм (n-s)-го рангу, у котрий входять ті (n-s) змінних, котрі зберігають однакові значення на цьому s-кубі. Для ДНФ значенню «1» відповідають прямі значення змінних, значенню «0» - їхні заперечення. Для КНФ значенню «0» відповідають прямі значення змінних, значенню «1» відповідають їхні заперечення. Змінні, що не зберігають свої значення на s-кубі, у мінтерм (макстерм для КНФ) не входять.
Задача мінімізації за допомогою карт Карно формулюється аналогічно задачі мінімізації на n-мірному кубі. Даний алгоритм мінімізації дає МДНФ для значень функції «1» чи МКНФ для значень функції «0».
Приклад. Карта Карно для функцій від однієї змінної f1=` x
(табл. 26.1), двох змінних f2=x1Úx2 (табл. 26.2), трьох змінних f3=`(x2`x3)Ú(x1`x2)Ú(`x1x2x3) (табл. 26.3) і чотирьох змінних f4=(x2`x3)Ú(x1`x2x4)Ú(`x1`x2x3) (табл. 26.4)
Таблиця 26.1
f1 x=0 1
Таблиця 26.2
f2 x1,x2 00 01 11 10
 1 1
|  1 1
|
Таблиця 26.3
 f3 x1,x2 x3 f3 x1,x2 x3
|  10 10
| |||
 1 1
| ||||
Таблиця 26.4
| f4 x1,x2 x3x4 | ||||
 1 1
| ||||
 1 1
| ||||
 1 1
| ||||
Використання карт Карно вимагає більш простих побудов (наочних), особливо у випадку функцій від 4-х змінних, у порівнянні з відображенням на n-вимірному кубі. Для відображення функцій 5-ти змінних використовуються дві карти Карно від 4-х змінних, для функцій 6-ти змінних використовуються чотири карти Карно, але при n³5 наочність карт Карно губиться.
Приклад. Дві карти Карно для функції від п'яти змінних, що відрізняються значенням x5 (табл. 26.5, 26.6),
f5=(`x2Ú`x4)ÙÙ(`x1Ú`x2Úx3)Ù(`x2Úx3Ú`x4)Ù(x1Úx2Úx3)Ù(`x1Ú`x3Ú`x4).
Таблиця 26.5
 f5 x1,x2 x3x4 f5 x1,x2 x3x4
|  11 11
| |||
 0 0
|  0 0
| |||
 0 0
| ||||
 11 11
| 
| |||
x5=0
Таблиця 26.6
 f5 x1,x2 x3x4 f5 x1,x2 x3x4
|  00 00
| |||

| ||||
 11 11
|  0 0
| |||

|
x5=1
Подібні картам Карно карти Вейча, що відрізняються іншим порядком проходження наборів та використовують позиційний код. Правила мінімізації для карт Вейча інші і не настільки наочні.
Приклад. Карта Вейча для функцій від трьох та п'яти змінних f6=(x1x2)Ú(x2`x3)Ú(`x1`x2x3), f7=(`x3`x5)Ú(`x1x2x4)Ú(x1x3`x4x5).
Таблиця 26.7
| f6 x1,x2 x3 |  01 01
| |||
 1 1
| ||||

 Таблиця 26.8
Таблиця 26.8
 f7 x1,x2,x3 x4,x5 f7 x1,x2,x3 x4,x5
| ||||||||
 00 00
| 
| 
| 
| |||||

|  0 0
| |||||||
Контрольні запитання
1. Як установлюється відповідність n-вимірного куба формулі булевої функції?
2. Що зіставляється конституенті одиниці або нуля у n-вимірному кубі?
3. Що зіставляється мінтерму або макстерму (n-k)-го рангу у n-вимірному кубі?
4. Що є s-кубами для n-вимірного куба?
5. Яка сукупність s-кубів є покриттям функції?
6. Як знайти мінімальне покриття функції?
7. Яка різниця у використанні графічного методу для КНФ?
8. Як виконується розмічування стовпців та рядків карти Карно і чому саме так?
9. Що відповідає конституенті одиниці або нуля у карті Карно?
10. Що відповідає мінтерму або макстерму (n-k)-го рангу у карті Карно?
11. Як виконується мінімізація за допомогою карти Карно?
12. Чи є якось обмеження у мінімізації за допомогою карти Карно?
13. Що є картою Вейча і як виконується мінімізація за допомогою карти Вейча?
 2015-06-28
2015-06-28 277
277







