Эйлеровы цепи, циклы, пути, контуры

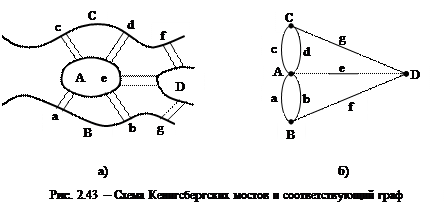
Эти понятия возникли в статье Эйлера в 1736 г., в которой он рассуждает о Кенигсбергских мостах. Известно, что Кенигсберг (ныне Калининград) расположен на берегах реки Преголи и островах на ней. Все части города соединены мостами. На рис. 2.43,а приведен план расположения семи мостов в Кенигсберге. Задача состоит в том, чтобы пройти каждый мост по одному разу и вернуться в исходную точку C.

Так как существенны только переходы через мосты, то план города можно свести к изображению графа, в котором ребра соответствуют мостам, а вершины – различным разделенным частям города (рис. 2.43,б).

Поскольку в конце обхода нужно вернуться в исходную часть города, и на каждом мосту нужно побывать по одному разу, этот маршрут является простым циклом, содержащим все ребра графа. В дальнейшем такие

циклы стали называть эйлеровыми, а графы, имеющие эйлеров цикл, – эйлеровыми графами.

Эйлеров цикл можно считать следом пера, вычерчивающего этот граф, не отрываясь от бумаги. Таким образом, эйлеровы графы – это графы, которые можно изобразить одним росчерком пера, причем процесс такого изображения начинается и заканчивается в одной и той же точке.

Обнаружив, что в данном графе не существует циклических обходов, проходящих по всем ребрам по одному разу, Эйлер обратился к общей задаче: при каких условиях в графе можно найти такой цикл? Ответ на этот вопрос дает следующая теорема.

Теорема 1 (Эйлера). Конечный связный неориентированный мультиграф является эйлеровым графом тогда и только тогда, когда в нем отсутствуют вершины нечетной степени.

Доказательство. Каждый раз, когда эйлеров цикл проходит через какую-либо вершину, он должен войти в нее по одному ребру, а выйти по другому. Поэтому условие отсутствия вершин нечетной степени в эйлеровом графе является необходимым.

Для доказательства достаточности предположим, что все вершины графа имеют четные степени. Начнем цепь P в произвольной вершине x_i графа G (рис. 2.44,а), и будем продолжать ее, насколько возможно, все время через новые ребра. Так как в каждой вершине число ребер четно, этот процесс может закончиться только в x_i. Если цикл P содержит не все ребра графа G, то удалим из G часть, соответствующую циклу P.

Графы P и G имеют четные степени всех вершин. То же должно быть справедливо и для оставшегося графа .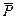

Так как граф G связен, в цикле P должна найтись вершина x_j, инцидентная также ребрам 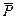. Из x_j можно построить новую цепь P¢, содержащую только ребра из 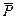. И снова такая цепь может закончиться только при возвращении в x_j. Но тогда из P и P¢ можно составить новый цикл

P₁= P(x_i, x_j) È P¢ È P(x_j, x_i),

который возвращается в x_i и содержит больше ребер, чем P. Если P₁ не является эйлеровым циклом, то построение повторяется. По окончании построения получим эйлеров цикл.

Процесс построения эйлерова цикла иллюстрирует рис. 2. 44, б. Объединяя,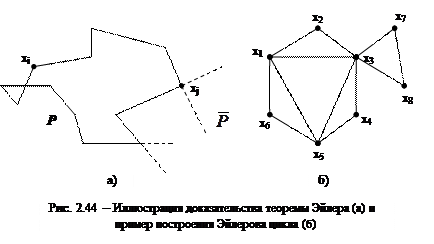
например, циклы {x₁,x₂, x₃, x₄, x₅,x₆, x₁} и {x₃,x₇, x₈, x₃,x₅, x₁,x₃}, получим эйлеров цикл { x₁,x₂, x₃, x₇, x₈, x₃,x₅, x₁,x₃, x₄, x₅,x₆, x₁}.

Как граф с эйлеровым циклом можно рассмотреть схему обхода выставки по различным коридорам, которую посетители должны пройти согласно указателям так, чтобы увидеть каждый экспонат по одному разу.

Эйлеровой цепью называется цепь, включающая все ребра данного конечного неориентированного графа G(X), но имеющая различные начало х_i и конец х_j. Чтобы в графе существовала эйлерова цепь, он должен быть связным и все вершины, кроме х_i и х_j должным иметь четные степени. Степени вершин х_i и х_j должны быть нечетными, что естественно, так как из х_i мы лишний раз выходим, а в х_j мы лишний раз входим. Эти условия являются достаточными для существования эйлеровой цепи.

Важен также следующий вопрос: каково наименьшее количество не пересекающихся по ребрам цепей, покрывающих конечный связный граф G(X) (покрыть– значит включить все ребра графа в цепь)? На этот вопрос отвечает теорема 2.

Теорема 2. В конечном связном неориентированном графе G(X) с k вершинами нечетной степени минимальное число непересекающихся по ребрам цепей, покрывающих G(X) равно k/2.

Доказательство. Пусть G(X) не является эйлеровым графом и k – число его вершин нечетной степени. Ранее было доказано, что k четно. Каждая вершина нечетной степени должна быть концом хотя бы одной из покрывающих граф цепей. Следовательно, число таких цепей не меньше, чем k/2. Но можно показать, что и не больше. Соединим попарно вершины нечетной степени k/2 ребрами. Тогда степень каждой вершины увеличиться на единицу и станет четной. Получится эйлеров граф, в котором существует эйлеров цикл. Теперь будем постепенно выбрасывать присоединенные ребра. При выбрасывании первого ребра эйлеров цикл превратится в эйлерову цепь, а при выбрасывании каждого последующего ребра одна из возникших к этому моменту цепей разобьется на две части. Таким образом, общее число этих цепей равно k/2.

В качестве примера рассмотрим граф на рис.2.45. В нем x₁, x₂, x₃, x₅ – вершины нечетной степени. Добавим два ребра: (x₂, x₅), (x₁, x₃) (штриховые линии). Получим эйлеров граф с эйлеровым циклом {x₁, x₂, x₃, x₄, x₅, x₂, x₅, x₆, x₁, x₃, x₁}. Убрав (x₃, x₁), получим эйлерову цепь. Убрав (x₂, x₅), получим 2 покрывающих цепи: {x₁, x₂, x₃, x₄, x₅, x₂} и {x₅, x₆, x₁, x₃}.

Из теоремы 2 следует, что если в связном неориентированном мультиграфе имеются две вершины нечетной степени х_i и х_j, то существует эйлерова цепь, начинающаяся в х_i и кончающаяся в х_j.

Если связный мультиграф G(X) имеет четыре вершины нечетной степени, то его можно нарисовать двумя росчерками. Если количество нечетных степеней равно k, то граф можно нарисовать k/2 росчерками.

Рассмотрим теперь случай конечного ориентированного графа. Чтобы в конечном ориентированном графе существовал эйлеров цикл (контур), необходимо и достаточно, чтобы полустепени исхода и захода вершин этого графа по входящим и исходящим дугам были равны:

m¢(x_i) = m¢¢(x_j), " x_i Î X.

Доказательство то же, что и для неориентированного графа.

Так как любому неориентированному графу соответствует ориентированный, в котором каждое ребро заменено двумя дугами, инцидентными тем же вершинам и идущими в противоположном направлении, то отсюда следует, что в конечном связном графе всегда можно построить ориентированный цикл, проходящий через каждое ребро по одному разу в каждом из двух направлений. Такой цикл называется способом обхода всех ребер графа. Он используется во многих прикладных задачах, связанных с графами.