Способы представления геометрических преобразований на плоскости

Рассмотрим следующую систему уравнений:

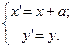
Эти уравнения можно интерпретировать двояким образом:

1. Все точки на плоскости ху перемещаются вправо на расстоя­ние а рис. 2.1.а.

2. Координатные оси х и у перемещаются влево на расстояние а рис. 2.1.б.

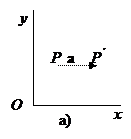Рис. 2.1. а) — перенос точек; б) — перенос системы координат

Этот простой пример иллюстрирует принцип, применимый и в более сложных ситуациях. Мы и далее будем рассматривать си­стемы уравнений, интерпретируя их либо как преобразования всех точек в фик­сированной системе координат, либо как изменение самой системы координат.

Пусть необходимо повернуть точку 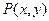вокруг начала ко­ординат О на угол. Изображение новой точки на рис. 2.2 обоз­начим через .

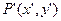Рис. 2.2. Поворот вокруг точки О на угол φ

Уравнения, задающие поворот точек на плоскости относительно начала координат:

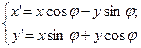
Эта система уравнений описывает поворот вокруг точки О — начала системы координат. Но часто это не то, что нам нужно. Если требуется выполнить поворот относительно заданной точки 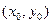, то в этих уравнениях можно заменить x на 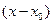, y на 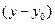, x ’ на, y ’ – на :

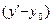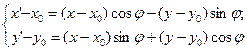
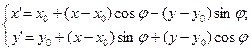
Система уравнений:

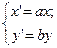
описывает изменение масштаба относительно точки О – начала системы координат. При этом координата x всех точек плоскости изменяется в a раз, а координата y – в b раз. Если a = b то искажения изображения объектов не происходит, и тогда говорят о равномерном масштабировании. В противном случае, изображение объектов искажается, и такое преобразование называется неравномерным масштабированием.

Если требуется выполнить масштабирование относительно заданной точки (x ₀, y ₀), то в этих уравнениях также можно заменить x на 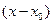, y на 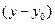, x ’ на 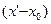, y ’ – на :

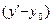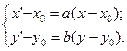
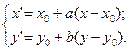
Система уравнений поворота точки относительно начала координат может быть записана в виде одного матричного уравнения:

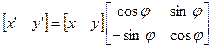
Можно записать в матричной форме и систему уравнений для масштабирования:

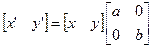
В ситуациях, когда совмещаются несколько преобразований, было бы удобно иметь единое матричное произведение для каждого элементар­ного преобразования. На первый взгляд это кажется невозмож­ным, если преобразование включает операцию переноса. Но, при использовании для представления точек на плоскости однородных координат, это реально.