Теоремы с доказательствами

1 2

Теорема о линейной независимости единичных векторов.
Теорема о том, что если любой вектор системы векторов можно представить в виде линейной комбинации ее линейно независимых векторов, то последние образуют базис этой системы.
Теорема о связи ранга системы векторов и ранга матрицы.
Теорема о связи ранга матрицы и ранга системы векторов.
Теорема о ранге линейного -мерного векторного пространства.
Необходимый и достаточный признак того, чтобы вектора образовывали базис в линейном -мерном векторном пространстве.
Доказательство того, что векторная форма системы 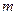линейных уравнений с неизвестными эквивалентна этой системе.
Теорема Кронекера – Капелли.
Следствие к теореме Кронекера – Капелли.
Теорема о том, что если ранг матрицы системы 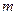линейных уравнений с неизвестными равен количеству её неизвестных, то система будет иметь единственное решение.
Метод Жордана-Гаусса.
Правило прямоугольника.