Определения и теоремы без доказательств
- Определение
-мерного вектора и его координат. - Определение нулевого вектора.
- Определение единичного вектора.
- Определение равных -мерных векторов.
- Определение суммы -мерных векторов.
- Определение произведения -мерного вектора на число.
- Определение разности -мерных векторов.
- Свойства действий над векторами.
- Определение вектора, противоположного вектору
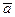. - Определение линейного -мерного векторного пространства.
- Определение линейной комбинации векторов.
- Определение линейно зависимых и независимых векторов.
- Критерий линейной зависимости векторов.
- Теорема Штейница.
- Определение ранга системы векторов.
- Определение базиса системы векторов.
- Теорема о том, что любой вектор системы векторов может быть представлен в виде линейной комбинации векторов ее базиса, причем единственным образом.
- Теорема о том, что если к системе векторов добавить вектор, являющийся линейной комбинации ее векторов, то ранг системы не изменится.
- Теорема о том, что если из системы векторов исключить вектор, являющийся линейной комбинации остальных ее векторов, то ранг системы не изменится.
- Теорема о том, что базисные строки (столбцы) матрицы линейно независимы.
- Теорема о том, что любая строчка (столбец) матрицы является линейной комбинацией ее базисных строк (столбцов).
- Определение ранга линейного -мерного векторного пространства.
- Два определения базиса линейного -мерного векторного пространства.
- Теорема о том, что любой вектор линейного -мерного векторного пространства может быть представлен в виде линейной комбинации векторов его базиса, причем единственным образом.
- Определение разложения вектора линейного -мерного векторного пространства по векторам его базиса.
- Определение координат вектора в базисе.
- Определение векторной формы системы
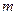линейных уравнений с неизвестными. - Определение решения векторной формы системы 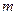линейных уравнений с неизвестными.
- Определение матрицы системы 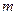линейных уравнений с неизвестными.
- Определение расширенной матрицы системы 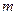линейных уравнений с неизвестными.
- Определение базисных и свободных переменных.
- Теорема о том, что если ранг матрицы системы 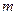линейных уравнений с неизвестными меньше количества её неизвестных, то система будет иметь бесконечное множество решений, причём...
- Определение элементарных преобразований над уравнениями.
- Определение эквивалентных систем 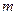линейных уравнений с неизвестными.
- Теорема о том, что если к системе уравнений применить элементарные преобразования над уравнениями, то в результате получится система, эквивалентная данной.
- Определение общего решения системы 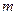линейных уравнений с неизвестными.
- Определение частного решения системы 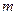линейных уравнений с неизвестными.
- Определение базисного решения системы 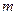линейных уравнений с неизвестными.
- Таблицы Гаусса.
- Определение главной и побочной диагонали прямоугольника.
- Алгоритм правила прямоугольника.
- Замечание 1 к правилу прямоугольника.
- Замечание 2 к правилу прямоугольника.
- Определение опорного решения.
- Алгоритм нахождения опорных решений.
- Замечание к алгоритму нахождения опорных решений.
2015-06-28
459
