Для гибкой опоры

Определение запаса устойчивости гибкой опоры

Газотурбинного двигателя

(алгоритм и инструкция к учебной программе)

Миколаїв 2012

Решение уравнения продольно ‑ поперечного изгиба

для гибкой опоры

При отсутствии распределенной нагрузки цилиндрический изгиб пластины может быть описан следующим дифференциальным уравнением четвертого порядка 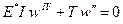[1]

(1)

В этом уравнении 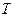– продольная сила; 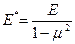– модуль Юнга для пластины.

Вводим обозначение 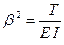, тогда

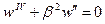(2)

Имеем следующие граничные условия

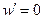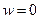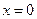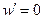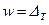; при ;

; при .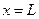

Используя подстановку 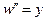, получим уравнение 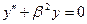, решение которого имеет вид 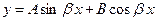или

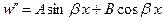. (3)

Проинтегрировав (3), получим 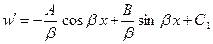. Используя граничное условие, запишем 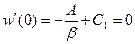, тогда

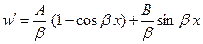. (4)

Проинтегрировав (4) получим 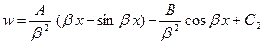. Используя граничное условие, запишем 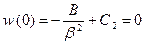, тогда

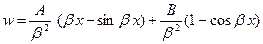. (5)

Применив граничные условия для случая 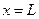, с помощью выражений (4) и (5) получим следующую систему уравнений

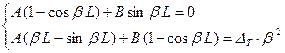
Главный определитель этой системы имеет вид

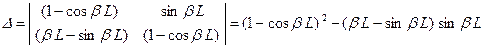. (6)

Определители для A и B имеют вид:

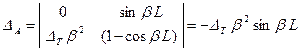; (7)

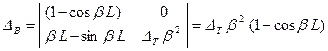. (8)

Преобразовав главный определитель (6) к виду

,

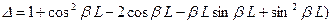получим 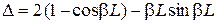. (9)

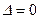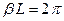Проанализируем (9) на ноль, получим при или .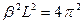

Тогда 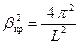или 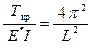. Для критической силы можно записать

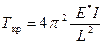. (10)

Коэффициенты для выражений (3), (4) и (5) будут иметь следующий вид

;

.

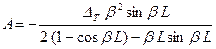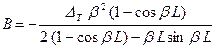Выражения для момента и прогиба можно записать в следующем виде

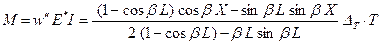; (11)

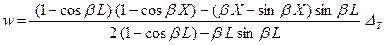. (12)