Машина Тьюринга

Доказательство алгоритмической неразрешимости определённых задач стало возможным после уточнения понятия алгоритма. В первой половине 20 века было предложено несколько таких уточнений, впоследствии оказавшихся эквивалентными. Все они исходят из того, что алгоритм можно рассматривать как отображение из множества описаний задач во множество результатов. Если элементы этих множеств закодировать целыми неотрицательными числами, то алгоритмический процесс представляет собой вычисление некоторой функции, аргументы и значение которой являются целыми неотрицательными числами. Функция называется вычислимой, если её значения могут быть вычислены с помощью алгоритма. Тогда существование невычислимых функций влечёт существование алгоритмически неразрешимых задач.

В 30 – е годы английским математиком Тьюрингом в качестве модели алгоритма было предложено гипотетическое вычислительное устройство, которое в определённой мере оказалось прототипом современных ЭВМ. Теперь его называют машиной Тьюринга (МТ).

МТ имеем конечное множество внутренних состояний Q = {q₀, q₁ ,..., q_m}, где q₁ считается начальным, а q₀ – конечным состояниями, а также внешнюю память в виде ленты, состоящей из конечного числа ячеек, в которых записаны символы из внешнего алфавита A = {a₀, a_1,..., a_n}, причём символ a₀ считается пустым и обычно обозначается как 0. В процессе работы МТ к существующим ячейкам могут пристраиваться новые пустые ячейки, так что лента является потенциально неограниченной в обе стороны.

В каждый из дискретных моментов времени МТ находится в одном из своих внутренних состояний и обозревает одну из ячеек ленты, воспринимая записанный в ней символ. В зависимости от внутреннего состояния и воспринимаемого символа в следующий момент МТ переходит в новое внутреннее состояние (возможно, то же самое), записывает новый символ в обозреваемую ячейку (возможно, тот же самый) и начинает обозревать соседнюю ячейку слева, либо ту же самую ячейку, либо соседнюю ячейку справа. Таким образом, функционирование МТ задаётся тремя функциями:

G: Q 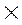A ® Q

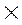F: Q A ® A

D: Q 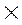A ® {L, C, R}.

Попав в заключительное состояние q₀, МТ прекращает работу.

Функции G, F, и D задаются набором команд или программой для МТ. Команды имеют вид q_i a_j ® q_k a_l s_p, где q_k = G(q_i a_j), a_i = F(q_i a_j), s_p = D(q_i, a_j).

В каждый момент времени состояние МТ полностью определяется внутренним состоянием q_i, содержимым ячеек ленты a_i1, a_i2 ,..., a_it и номером k обозреваемой ячейки, что в совокупности называется конфигурацией и может быть записано как a_i1 a_i2 ,..., a_ik-1

q_i a_ik a_ik+1... a_it.

Конфигураций, получающиеся из данной приписыванием слева или справа произвольного числа пустых ячеек, считаются эквивалентными. В процессе работы МТ происходит последовательная смена конфигураций. Начальная конфигурация должна быть задана. Тогда все последующие конфигурации определяются программой. Если условиться считать, что в начальный момент машина находится в состоянии q₁ и обозревает самую левую ячейку ленты, то начальная конфигурация полностью задаётся начальным словом – набором записанных в ячейках ленты символов.

Начав работу с некоторого начального слова, МТ либо остановится через конечное число шагов, либо никогда не остановится. В первом случае говорят, что МТ применима к слову Р, а во втором, - что не применима.

Перейдём к рассмотрению примеров. Будем использовать внешний алфавит из двух символов A = {0, 1}. Если Р – некоторое слово, то для слова P P...P (m раз) будем для краткости использовать обозначение [P]^m. Так, например, слово 1100011000111 запишется как [1² 0³]² 1³.

Пусть МТ с тремя внутренними состояниями q_0, q₁ и q₂ задаётся программой:

q₁ 0 ® q₁ 0R

q₁ 1 ® q₂ 0R

q₂ 1 ® q₁ 0R

q₂ 0 ® q₀ 1C.

Пусть начальное слово P = 1³ 01. Тогда при работе МТ последовательно возникают конфигурации: q₁ 1³ 01, q₂ 1² 01, q₁ 101, q₂ 01, q₀ 1².

МТ остановилась, перейдя в заключительное состояние q_0, т.е. МТ применима к данному слову.

Пусть теперь начальное слово p = 1⁴. Тогда последовательными конфигурациями будут:

q₁ 1⁴, q₂ 1³, q₁ 1², q₂ 1, q₁ 0, q₁ 0, q₁ 0,….

МТ никогда не остановится, т.е. МТ не применима к данному слову.

Пусть теперь требуется построить МТ, прибавляющую к данному неотрицательному целому числу единицу, т.е. МТ должна переводить конфигурацию q₁ 1ⁿ в q₀ 1ⁿ⁺¹. Вот такая МТ:

q₁ 1 q₁ 1 R

q₁ 0 q₂ 1 L

q₂ 1 q₂ 1 L

q₂ 0 q₀ 0 R.

Пусть теперь требуется решить задачу удвоения числа, т.е. q₁ 1ⁿ ® q₀ 1²ⁿ. Эта задача может быть решена с помощью такой МТ:

q₁ 1 ® q₂ 0R

q₂ 1 ® q₃ 1 L

q₃ 0 ® q₄ 0 L

q₄ 1 ® q₄ 1 L

q₄ 0 ® q₅ 1R

q₅ 1 ® q₅ 1R

q₅ 0 ® q₁ 1R

q₂ 0 ® q₆ 1 L

q₆ 1 ® q₆ 1 L

q₆ 0 ® q₀ 1C.

Идея алгоритма состоит в том, что в заданном слове 1ⁿ вводится маркерный 0, который в ходе работы алгоритма передвигается слева направо. При каждом его передвижении слева к слову приписывается 1. МТ завершает работу, когда маркерный 0 достигает правого конца исходного слова.