Задание №1.
Доказать равенство множеств:
а) исходя из определения равенства множеств;
б) Преобразуя левую (или правую) часть равенства в правую часть (соответственно, в левую);
в) используя характеристические функции и представляя множества с помощью булевых векторов.
1.6. (A 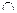 B)
B) 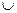 (C
(C 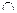 D)=(A
D)=(A 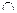 C)
C) 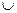 (B
(B 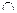 C)
C) 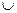 (A
(A 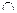 D)
D) 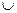 (B
(B 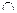 D)
D)
Задание №2.
на множестве А(в каждом варианте А – конкретное множество) задано бинарное отношение 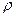 . Какими из свойств (рефлективность, симметричность, транзитивность и т.д.) оно обладает?
. Какими из свойств (рефлективность, симметричность, транзитивность и т.д.) оно обладает?
2.6. а) А – множество действительных чисел и для любых x, y 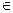 А имеем
А имеем 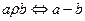 - рациональное число.
- рациональное число.
б) А – множество положительных действительных чисел и для любых x, y 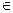 А
А 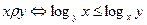 .
.
Задание №3.
На множестве 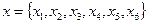 с помощью булевой матрицы задать бинарное отношение
с помощью булевой матрицы задать бинарное отношение 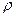 , которое одновременно обладает следующими свойствами.
, которое одновременно обладает следующими свойствами.
3.6. 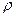 рефлексивно, симметрично и не транзитивно.
рефлексивно, симметрично и не транзитивно.
 2015-06-28
2015-06-28 516
516








