Система ФАЛ {f1, f2,…, fn} называется полной в некотором классе функций, если любая функция из этого класса может быть представлена суперпозицией этих функций.
Система ФАЛ, являющаяся полной в некотором классе функций, называется базисом.
Минимальным базисом называется такой базис, для которого удаление хотя бы одной из функций fi, которые его образуют, превращает эту систему функций в неполную.
Любая функция может быть представлена с помощью элементарных функций {, &, Ú}. Эта система ФАЛ образует универсальный базис.
Наиболее популярными в алгебре логики являются базисы {Ú,}, {&,}, {¯}, {|}, которые являются минимальными.
Например:
Представить функцию 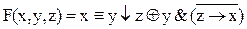 в базисах
в базисах
{Ú, Ø}, {|}. Для проверки результата составить таблицу истинности.
Решение:
Для перевода в базис {Ú, Ø} применим закон де Моргана к ДСНФ функции: 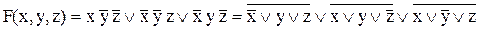 .
.
Для перевода функции в базис {|} применим следующие соотношения к ДСНФ функции:
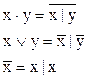
Обозначим 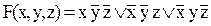
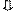
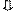
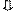
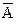
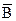
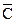
Выполним перевод в базис {|} по действиям.
1. 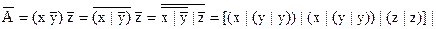
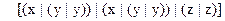
2. 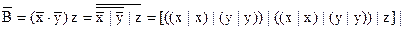
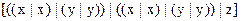
3. 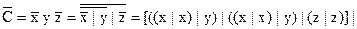
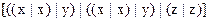
4. 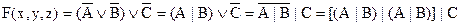
Проверим преобразования с использованием таблицы истинности:
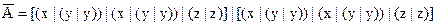
2 1 3 5 4 6
Таблица истинности для выражения 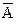 :
:
| № | x | y | z | y | y | x | (y | y) | z | z | 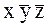 | |||
Аналогично, проверяем 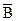 и
и 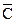 .
.
Для проверки, построим таблицу истинности для полученной формы функции F(x, y, z).
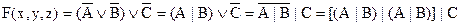
Таблица истинности для F(x,y,z)
| № | x | y | z | 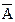 | 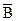 | 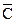 | A | B | C | A | B | 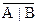 | 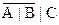 | |
Cтолбцы, соответствующие функции F(x, y, z) в таблицах истинности равны, следовательно, преобразования выполнены правильно.
Задание к лабораторной работе
1. По заданному варианту, составить таблицу истинности функции трех переменных F(x,y,z). Изобразить графически F(x,y,z) на кубе.
2. Построить ДСНФ и КСНФ.
3. Используя законы алгебры логики, пошагово преобразовать заданную функцию в ДНФ. Построить таблицу истинности.
4. Наиболее простую аналитическую форму перевести в базисы {Ø,Ú}, {Ø,&}, {|}, {¯} и сравнить с заданной функцией, построив таблицу истинности.
1. 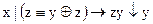 2. 2. 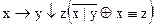 3. 3. 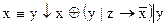 4. 4. 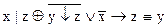 5. 5. 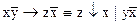 6. 6. 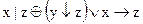 7. 7. 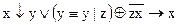 8. 8. 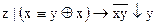 9. 9. 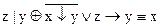 10. 10. 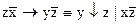 11. 11. 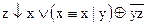 12. 12. 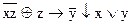 13. 13. 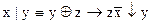 14. 14. 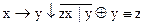 15. 15. 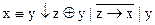 | 16. 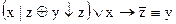 17. 17. 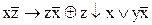 18. 18. 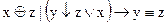 19. 19. 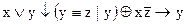 20. 20. 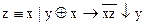 21. 21. 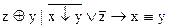 22. 22. 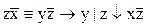 23. 23. 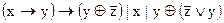 24. 24. 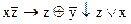 25. 25. 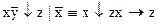 26. 26. 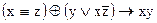 27. 27. 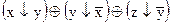 28. 28. 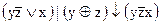 29. 29. 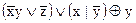 30. 30. 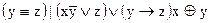 |
Контрольные вопросы
1. Определение двоичного набора.
2. Определение булевой функции или функции алгебры логики (ФАЛ).
3. Область определения и область значений ФАЛ.
4. ФАЛ от одной переменной.
5. Элементарные ФАЛ от двух переменных.
6. Основные законы алгебры логики.
7. Полные системы функций, минимальный базис.
8. Аналитическое описание ФАЛ: дизъюнктивная и конъюнктивная нормальные формы.
Лабораторная работа № 4
 2015-06-28
2015-06-28 1347
1347








