Означення. Скалярним добутком 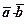 двох векторів
двох векторів 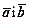 (позначається
(позначається 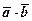 ) називається число рівне добуткові модулів цих векторів, помноженому на косинус кута між ними:
) називається число рівне добуткові модулів цих векторів, помноженому на косинус кута між ними:
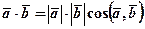 . (1)
. (1)
На основі властивості 1 проекцїї вектора рівність (1) запишеться:
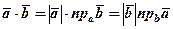 (2)
(2)
У фізиці робота А сталої сили 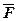 при прямолінійному переміщенні вздовж вектора шляху
при прямолінійному переміщенні вздовж вектора шляху 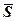 знаходиться як скалярний добуток цих векторів:
знаходиться як скалярний добуток цих векторів:
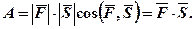
Основні властивості скалярного добутку.
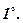 Скалярний добуток комутативний
Скалярний добуток комутативний
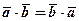 .
.
Випливає із (1).
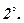 Числовий множник
Числовий множник 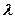 можна виносити за знак скалярного добутку:
можна виносити за знак скалярного добутку:
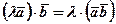 .
.
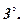 Для довільних векторів
Для довільних векторів 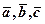
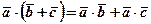 .
.
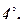 Скалярний добуток двох векторів
Скалярний добуток двох векторів 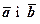 дорівнює нулю (
дорівнює нулю (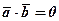 ) тоді і тільки тоді, коли один із них є нульовим вектором, або коли ці вектори перпендикулярні
) тоді і тільки тоді, коли один із них є нульовим вектором, або коли ці вектори перпендикулярні 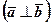 .
.
Таблиця скалярного множення ортів. Згідно означення (1) 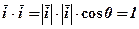 , аналогічно
, аналогічно 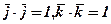 , а за властивістю (4)
, а за властивістю (4) 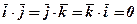 .
.
Отже, скалярний добуток одноіменних ортів дорівнює одиниці, а різноіменних - 0.
Скалярний добуток векторів в координатній формі. Якщо 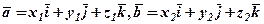 , то
, то 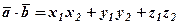 .
.
Дійсно, за допомогою властивостей 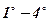 маємо
маємо
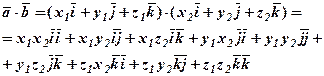
Оскільки добуток одноіменних ортів дорівнює 1, а різноіменних – 0, то отримуємо формулу скалярного добутку у координатній формі:
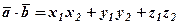 . (3)
. (3)
Приклад 1. Знайти скалярний добуток векторів 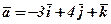 і
і 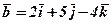 .
.
Розв’язання: За формулою (3) маємо:
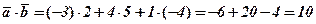 .
.
Приклад 2. Задані точки А(3,2,3), В(1,-4,3), С(-4,5,1). Знайти скалярний добуток векторів 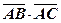 .
.
Розв’язання. Спочатку знайдемо вектори 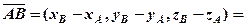
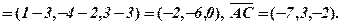
За формулою (3) маємо
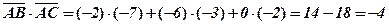 .
.
Довжина вектора. Якщо в (1) 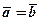 , то
, то
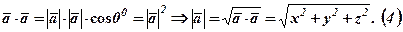
Відстань між двома точками. 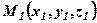 і
і 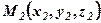 знаходиться як довжина вектора
знаходиться як довжина вектора 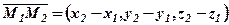 за формулою (4):
за формулою (4):
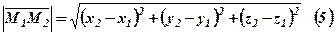
Косинус кута між двома векторами отримаємо із формули (1) із врахуванням (3) і (4):
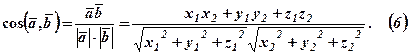
Приклад 3. Задані точки 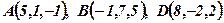 . Для паралелограма, побудованого на векторах
. Для паралелограма, побудованого на векторах 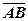 і
і 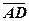 обчислити: 1)довжини сторін, тобто
обчислити: 1)довжини сторін, тобто 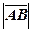 і
і 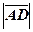 ; 2) косинус та синус, кута
; 2) косинус та синус, кута 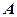 ; 3) площу.
; 3) площу.
Розв’язання. Знаходимо вектори 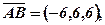
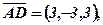 тоді: 1)
тоді: 1) 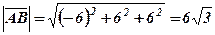 ,
, 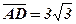 . 2)
. 2) 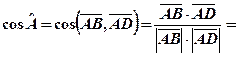
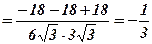 (кут
(кут 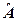 - тупий),
- тупий), 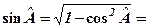
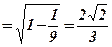 . 3)
. 3) 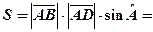
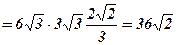 .
.
Приклад 4. Знайти модуль вектора 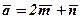 , якщо
, якщо
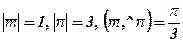 .
.
Розв’язання. За формулою (4) 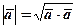 . Знаходимо
. Знаходимо
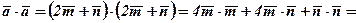
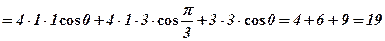 ,
,
тоді 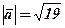 .
.
Умова перпендикулярності двох ненульових векторів 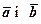 випливає із властивості 4° і формули (3)
випливає із властивості 4° і формули (3)
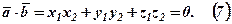
Проекція вектора на вектор знаходиться із врахуванням (3) і (4):
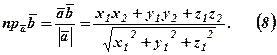
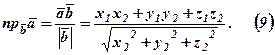
Теорема. Декартові прямокутні координати 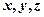 вектора
вектора 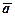 в базисі
в базисі 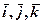 є його проекціями на відповідні осі координат.
є його проекціями на відповідні осі координат.
Дійсно, згідно з (9) маємо
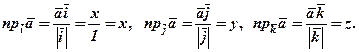
Напрямними косинусами вектора 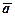 називаються косинуси кутів
називаються косинуси кутів 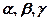 , утворених між вектором
, утворених між вектором 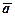 та координатними осями ОХ, ОУ, ОZ (див. рис. 19)
та координатними осями ОХ, ОУ, ОZ (див. рис. 19)
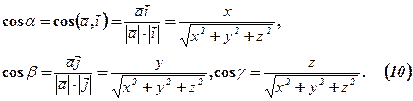
Приклад. Знайти напрямні косинуси вектора 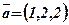 та значення виразу
та значення виразу 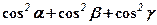 .
.
Розв’язання. 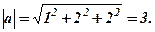
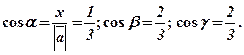
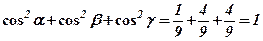 .
.
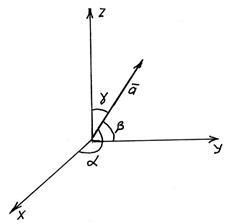
Рис. 19
Легко перевірити, що для довільного вектора 
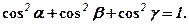
Напрямні косинуси вектора 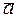 повністю визначають напрямок вектора і є координатами одиничного вектора
повністю визначають напрямок вектора і є координатами одиничного вектора 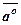 , що збігається за напрямком з
, що збігається за напрямком з 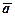 , тобто:
, тобто:
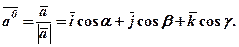
 2015-06-28
2015-06-28 620
620








