Задана функция y=f(x). Требуется:
1. используя логические функции, построить схематичный график f(x) на заданном отрезке локализации в виде точечной диаграммы;
2. используя средство подбора параметра, найти на этом отрезке все корни уравнения f(x)=0 с заданной точностью.
Номер варианта – предпоследняя цифра шифра. Варианты заданий приведены в таблице.
| N Вар. | f(x) | Отрезок локализации | Точность |
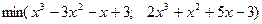 | [-4; 4] | 0,0001 | |
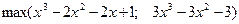 | [-5; 5] | 0,00001 | |
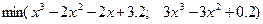 | [-5; 4] | 0,0001 | |
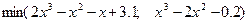 | [-4; 5] | 0,00001 | |
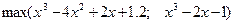 | [-5; 5] | 0,000001 | |
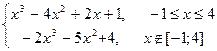 | [-5; 5] | 0,00001 | |
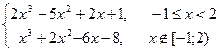 | [-6; 4] | 0,0001 | |
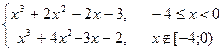 | [-5; 4] | 0,00001 | |
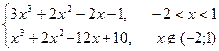 | [-5; 3] | 0,00001 | |
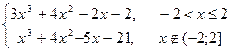 | [-5; 5] | 0,000001 |
Рекомендуется придерживаться следующего порядка:
1. установить требуемую точность вычислений;
2. построить схематичный график функции f(x) на отрезке локализации; при составлении формулы обязательно использование необходимых логических функций;
3. проградуировать ось значений таким образом, чтобы на графике отображались только те его части, где график пересекает ось x;
4. по графику найти приближенные значения к корням уравнения;
5. при помощи средства подбора параметра (там, где это необходимо) уточнить найденные приближенные значения корней.
При оформлении решения в электронной таблице рекомендуется придерживаться образца, приведенного на рис. 4.

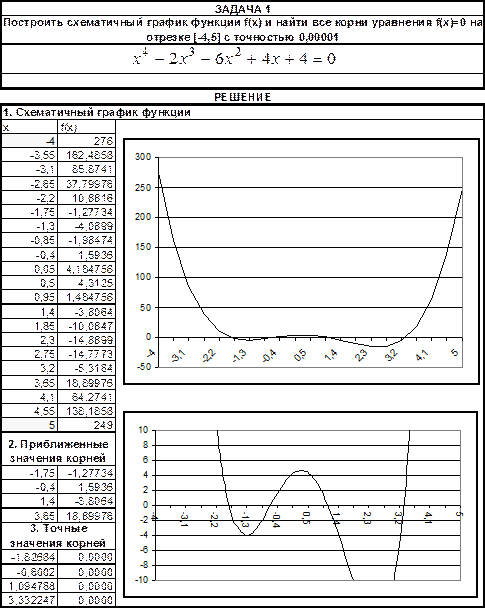
Рис. 4.
 2015-06-28
2015-06-28 960
960







