Задания к экзамену по дисциплине «Высшая математика»
Для студентов I курса весеннего семестра
заочной (обычной) формы обучения ФЭФ
Раздел 1. Интегральное исчисление
1. Найти неопределенный интеграл:
а) используя таблицу и свойства интегралов:
1) 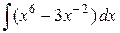 ; Ответ:
; Ответ: 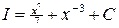 .
.
2) 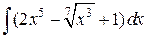 ; Ответ:
; Ответ: 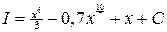 .
.
3) 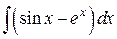 ; Ответ:
; Ответ: 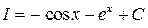 .
.
4) 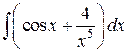 ; Ответ:
; Ответ: 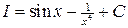 .
.
5) 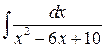 ; Ответ:
; Ответ: 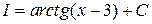 .
.
6) 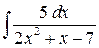 ; Ответ:
; Ответ: 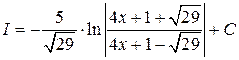 .
.
б) используя метод подстановки (замену переменной):
1) 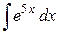 ; Ответ:
; Ответ: 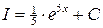 .
.
2) 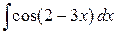 ; Ответ:
; Ответ: 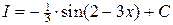 .
.
3) 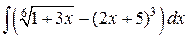 ; Ответ:
; Ответ: 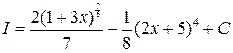 .
.
4) 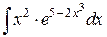 ; Ответ:
; Ответ:  .
.
5) 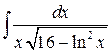 ; Ответ:
; Ответ: 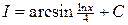 .
.
в) используя метод интегрирования по частям:
1) 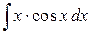 ; Ответ:
; Ответ: 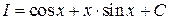 .
.
2) 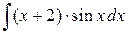 ; Ответ:
; Ответ: 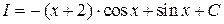 .
.
3) 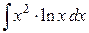 ; Ответ:
; Ответ: 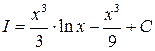 .
.
4) 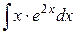 ; Ответ:
; Ответ: 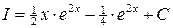 .
.
2. Вычислить площадь плоской фигуры, ограниченной линиями:
1) 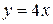 ,
, 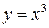 ,
, 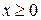 ; Ответ:
; Ответ: 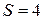 кв.ед.
кв.ед.
2) 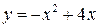 ,
, 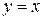 ; Ответ:
; Ответ:  кв.ед.
кв.ед.
3) 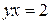 ,
, 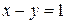 ,
, 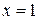 ; Ответ:
; Ответ: 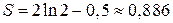 (кв.ед.).
(кв.ед.).
3. 1) Определить объем продукции, произведенной рабочим за первый час рабочего дня, если производительность труда характеризуется функцией 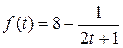 .
.
Ответ: 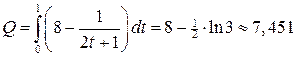 (ед.).
(ед.).
2) Определить объем продукции, произведенной рабочим за второй час рабочего дня, если производительность труда характеризуется функцией 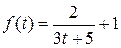 .
.
Ответ: 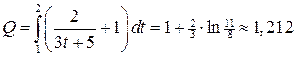 (ед.).
(ед.).
4**.
1) Вычислить 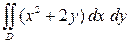 , если область
, если область 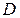 ограничена линиями:
ограничена линиями: 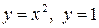 .
.
|
|
|
Ответ: 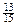 .
.
2) Вычислить 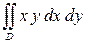 , если область
, если область 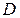 ограничена линиями:
ограничена линиями: 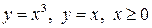 .
.
Ответ: 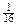 .
.
Раздел 2. Функции нескольких переменных (ФНП)
1. Найти значения частных производных первого порядка функции 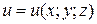 в точке
в точке 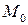 . Найти дифференциал первого порядка в общем виде.
. Найти дифференциал первого порядка в общем виде.
1) 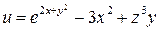 ,
, 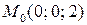 .
.
Ответ: 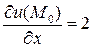 ;
; 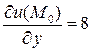 ;
; 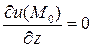 ;
;
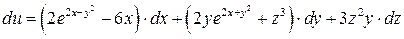 .
.
1) 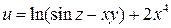 ,
, 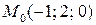 .
.
Ответ: 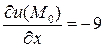 ;
; 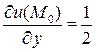 ;
; 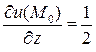 ;
;
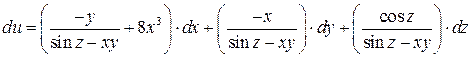 .
.
2**. Исследовать на экстремум функции:
1) 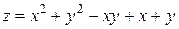 ; Ответ:
; Ответ: 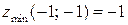 .
.
2)  ; Ответ:
; Ответ: 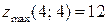 .
.
1) 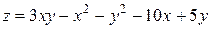 ; Ответ: точек экстремума нет.
; Ответ: точек экстремума нет.
3**. Найти наибольшее и наименьшее значения функции 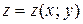 в замкнутой области
в замкнутой области 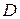 , ограниченной линиями:
, ограниченной линиями:
1) 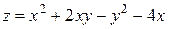 , если
, если 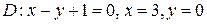 .
.
Ответ: 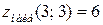 ,
, 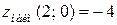 .
.
2) 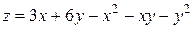 , если
, если 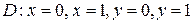 .
.
Ответ: 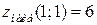 ,
, 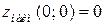 .
.
3) 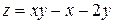 , если
, если 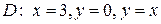 .
.
Ответ: 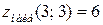 ,
, 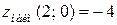 .
.
4. Для функции 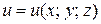 найти градиент в точке
найти градиент в точке 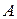 .
.
1) 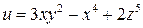 ,
, 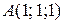 . Ответ:
. Ответ: 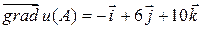 .
.
2) 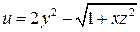 ,
, 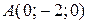 . Ответ:
. Ответ: 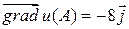 .
.
Раздел 3. Дифференциальные уравнения (ДУ)
1. Найти общее решение или общий интеграл для ДУ с разделяющимися переменными:
1) 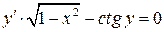 . Ответ:
. Ответ: 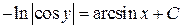 .
.
2) 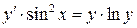 . Ответ:
. Ответ: 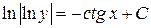 .
.
3) 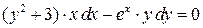 . Ответ:
. Ответ: 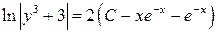 .
.
2**. Найти общее решение или общий интеграл для однородного ДУ:
1) 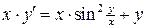 . Ответ:
. Ответ: 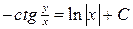 .
.
2) 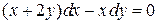 . Ответ:
. Ответ: 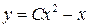 .
.
3) 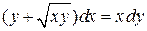 . Ответ:
. Ответ: 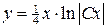 .
.
3**. Найти общее решение или общий интеграл для линейного ДУ:
1) 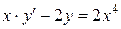 . Ответ:
. Ответ: 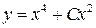 .
.
2) 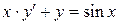 . Ответ:
. Ответ: 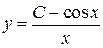 .
.
3) 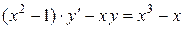 . Ответ:
. Ответ: 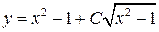 .
.
4. Решить дифференциальное уравнение:
1) 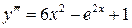 . Ответ:
. Ответ: 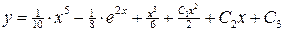 .
.
2) 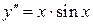 . Ответ:
. Ответ: 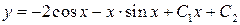 .
.
5. Решить задачу Коши для ЛОДУ второго порядка при начальных условиях:
1) 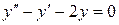 при начальных условиях
при начальных условиях 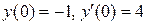 .
.
Ответ: 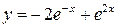 .
.
2) 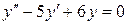 при начальных условиях
при начальных условиях 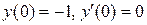 .
.
Ответ: 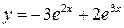 .
.
Раздел 4. Ряды
1. Исследовать на сходимость числовой ряд, используя:
1) признак Даламбера 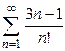 ; Ответ: сходится.
; Ответ: сходится.
2) признак Даламбера 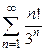 ; Ответ: расходится.
; Ответ: расходится.
3) признаки сравнения 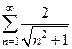 ; Ответ: расходится.
; Ответ: расходится.
4) признаки сравнения 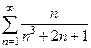 ; Ответ: сходится.
; Ответ: сходится.
5) радикальный признак Коши 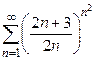 . Ответ: расходится.
. Ответ: расходится.
6) радикальный признак Коши 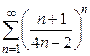 . Ответ: сходится.
. Ответ: сходится.
2**. Исследовать на сходимость знакочередующийся ряд
|
|
|
1) 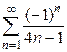 . Ответ: сходится условно.
. Ответ: сходится условно.
2) 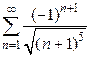 . Ответ: сходится абсолютно.
. Ответ: сходится абсолютно.
3) 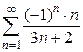 . Ответ: расходится.
. Ответ: расходится.
3**. Найти область сходимости степенного ряда
1) 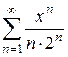 . Ответ:
. Ответ: 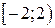 .
.
2) 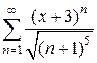 . Ответ:
. Ответ: 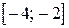 .
.
 2015-06-24
2015-06-24 290
290






