Фундаментальная система разрезов

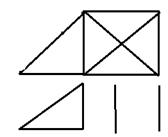
Насколько связан связный граф? Если в графе есть цикл, то он более связан, чем дерево. С другой стороны, если в графе есть мосты, то связность его (в мостах) такая же, как и у дерева. Мера связности графа – сколько рёбер графа надо удалить, чтобы он перестал быть связным.

Разделяющим множеством (иногда разрезом) связного графа называется такое множество рёбер, удаление которых приводит к несвязному графу.

Например, в данном графе каждое из множеств {1,2,5} и {3,6,7,8} является разделяющим.

Разрезом (сечением) (правильным, простым разрезом) называется разделяющее множество, никакое собственное подмножество которого не является разделяющим. ({1,2})

Любой разрез является надмножеством правильного разреза.

Мостом называется разрез, состоящий из одного ребра.

Рассмотрим некоторый остов Т графа G(V, E_T). Возьмём ребро остова е Î E_T и определим разрез S_e следующим образом. Ребро е – мост в дереве E_T. Следовательно, удаление ребра е разбивает всё множество вершин графа на два подмножества V₁ и V₂ так, что V₁, V₂ Î V; V₁, V₂ ¹Æ; V₁ÇV₂ = V, V₁ÈV₂ = Æ. Включим в разрез S_e ребро е и все хорды остова E_Т, которые соединяют вершины множества V₁ с вершинами множества V₂:

S_e ƒ e Ç {(v₁, v₂)ÎT*|v₁ ÎV₁ & v₂ Î V₂} = E(V₁, V₂).

Тогда S_e – простой разрез. Система разрезов S ƒ { S_e } _eÎT называется фундаментальной системой разрезов (коциклов), а сами разрезы системы называются фундаментальными. Количество разрезов в данной фундаментальной системе называется коциклическим рангом (или коцикломатическим числом) графа G и обозначается С*(G).

Замечание. Между циклами и разрезами существует определённая двойственность, поэтому разрезы иногда называют коциклами. Отсюда все названия с приставкой «ко».

Теорема. Любой правильный разрез в связном графе можно представить как симметрическую разность некоторых фундаментальных разрезов из системы ’, определяемой произвольным остовом Т.

Следствие. Количество разрезов в фундаментальной системе равно числу рёбер остова: С*(G) = n–1.

Рассмотрим векторное пространство над двоичной арифметикой, натянутое не множество рёбер Е графа G. Элемент этого векторного пространства – линейную комбинацию рёбер можно отождествить с подмножеством рёбер – как это делалось в предыдущем разделе. При такой интерпретации сложению рёбер соответствует симметрическая разность множества рёбер. Множества циклических векторов и множество правильных разрезов замкнуты относительно симметрической разности, а потому являются подпространствами общего пространства подмножеств рёбер графа. Каждое из этих подпространств является линейным дополнением другого.