Пороговая оптимизация

На множестве всех возможныхпутей графа 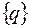, соединяющих первую вершину с последней, определим понятие j -й длины пути (j =1, q) по k -му критерию оптимизации 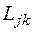: это сумма значений k -го критерия по всем вершинам j -го пути.

Пороговая оптимизация выполняется в виде следующих шагов.

1) Назначают главный 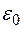и множество второстепенных критериев оптимизации 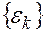, k =1, m-1 и присваивают их каждой вершине графа (операции): 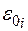, , 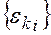k =1, m-1.

2)Определяем множество 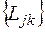, j= 1 ,q, k= 1 ,m с помощью программы AMACONT, выбрав в качестве основного критерия - критерий 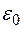[2]. В результате получается полный перечень путей графа, отсортированный в порядке возрастания основного критерия .

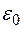3) Для каждого k -го второстепенного критерия экспертно назначается ограничение (порог) на длину пути .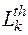

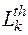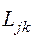
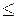
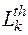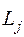
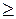
4) Пороговое значение отсекает часть множества q всех путей графа: путь отсекается – вычеркивается из перечня, полученного в п.2, если хотя бы по одному из второстепенных критериев оптимизации он не удовлетворяет неравенству - если оптимизация k -го критерия предусматривает его минимизацию и неравенству 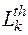если оптимизация k -го критерия предусматривает его максимизацию.

Неравенства могут быть строгими – в том случае, если длина пути, равная пороговой не включается в множество путей, прошедших порог.

5)Таким образом, множество всех путей q проверяется на соответствие ограничениям по каждому из второстепенных критериев. Остаются лишь те пути, которые удовлетворяют всем ограничениям, т.е. прошли пороги по всем второстепенным критериям. Обозначим это множество .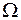

6)На множестве 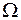проводим однокритериальную оптимизацию по программе AMACONT, т.е. из множества путей 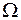выбираем тот, который содержит наилучший показатель основного (главного) критерия (к примеру, если это себестоимость С, то минимальное значение)