Найти решение самого широкого круга оптимизационных задач в логистике позволяет использование моделей линейного и целочисленного программирования, рассмотренные нами выше. Задача маршрутизации автотранспортных средств осуществляется простыми и эффективными методами эвристики (приближенными методами), позволяющими быстро найти нужное решение. Однако они не гарантируют нахождение оптимального решения. В настоящее время разрабатываются методы, которые объединяют гибкость эвристики и строгость моделей линейного программирования, что позволяет получить оптимальное или, по крайней мере, доказуемо лучшее решение. Один из эффективных методов, позволяющих находить оптимальное решение при маршрутизации перевозок мелкопартионных грузов, предложенный Дж. Шапиро, получил название унифицированной методики оптимизации.
На рис. 19 представлена логика унифицированной методики оптимизации для задачи локальных поставок. Сначала используют методы эвристики для создания одного или более возможных решений маршрутизации, т.е. набора допустимых развозочных или сборных маршрутов. В качестве стоимости решения рассматриваются общие транспортные издержки, которые могут рассчитаны различными способами, например, представлять собой сумму постоянных (накладных) затрат за определенный период (например, за день) для каждой единицу подвижного состава и переменных затрат на 1 километр пробега. Затем переходят к модели линейного программирования, содержащей допустимые маршруты, созданные с помощью эвристики, и оптимизируют ее. Эта модель ищет пути минимизации общей стоимости маршрутов, требующих посещения клиентов лишь один раз, но и дает нереальные комбинации, такие как «использование 0,4 маршрута j и 0,6 маршрута k». Для исключения дробных частей используется модель целочисленного программирования, оптимизация которой позволяет получить строгое решение задачи маршрутизации автотранспортных средств.
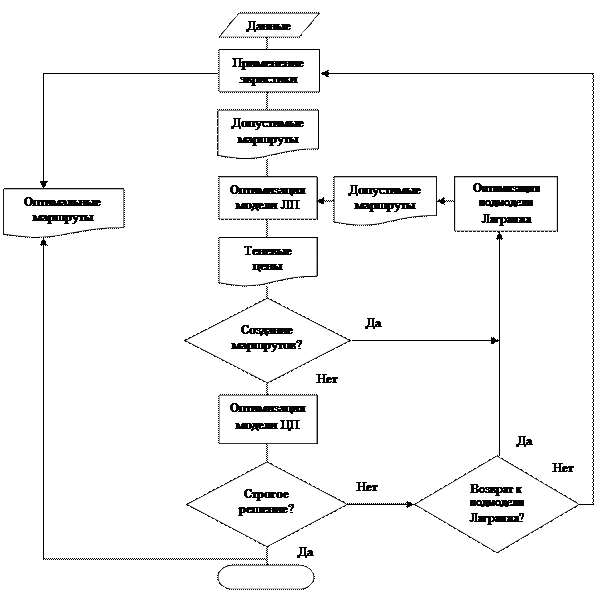
Рис. 19. Логика унифицированной методики оптимизации
Наряду с эвристикой при формировании допустимых маршрутов используются возможности линейного программирования, точнее строится и оптимизируется модель двойственная к основной модели линейного программирования. Первоначально в нее включаются все допустимые маршруты, найденные с помощью эвристики. Оптимизация этой модели заключается в максимизации общего вознаграждения за включение допустимых маршрутов в окончательное решение. Вознаграждение равно разнице валового дохода и затрат маршрута. Валовой доход равен сумме двойственных (теневых) цен для обслуженных клиентов. Если общее вознаграждение конкретного маршрута положительно, то этот маршрут добавляется в модель линейного программирования. С другой стороны, если общее вознаграждение равно нулю, то можно сказать, что нет допустимых маршрутов для добавления в модель линейного программирования.
Двойственную модель ЛП, как уже было отмечено, строят и оптимизируют в том случае, если для формирования дополнительных маршрутов используются возможности линейного программирования. Если же дополнительные маршруты созданы средствами Деловой карты, то необходимость создания и оптимизации двойственной модели ЛП отсутствует.
Создаваемая нами модель ЛП, включающая допустимые маршруты, является вариантом модели назначений. Модель назначений часто встречается в разнообразных управленческих ситуациях, связанных с распределением n неделимых агентов или объектов по n заданиям.
Предположим, мы имеем множество клиентов 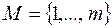 , для обслуживания которых можем задействовать множество автомобилей
, для обслуживания которых можем задействовать множество автомобилей 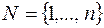 . Введем в рассмотрение переменные
. Введем в рассмотрение переменные 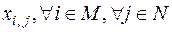 , принимающие значение
, принимающие значение 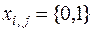 . Очевидно, что
. Очевидно, что 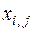 принимает значение 1, если i -й клиент включен в маршрут j -го автомобиля, и значение 0, если i -й клиент не включен в маршрут j -го автомобиля. Введем дополнительные переменные
принимает значение 1, если i -й клиент включен в маршрут j -го автомобиля, и значение 0, если i -й клиент не включен в маршрут j -го автомобиля. Введем дополнительные переменные 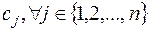 , представляющие собой затраты на транспортировку на j -м маршруте, и
, представляющие собой затраты на транспортировку на j -м маршруте, и 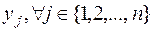 , принимающие значения:
, принимающие значения:
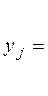 1, если j -й маршрут включен в оптимальный вариант,
1, если j -й маршрут включен в оптимальный вариант,
0, если j -й маршрут не включен в оптимальный вариант.
Формируемая нами модель линейного программирования отличается от рассмотренной выше классической модели задачи о назначениях. Отличие заключается, прежде всего, в том, что каждый автомобиль может обслуживать несколько заказов клиентов, следовательно, сумма по столбцам для булевой матрицы переменных 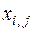 , в данном случае, не равна 1. Другое существенное отличие заключается в том, что булева матрица переменных
, в данном случае, не равна 1. Другое существенное отличие заключается в том, что булева матрица переменных 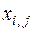 уже сформирована, т.к. мы имеем набор маршрутов, рассчитанных и проложенных средствами Деловой карты.
уже сформирована, т.к. мы имеем набор маршрутов, рассчитанных и проложенных средствами Деловой карты.
Таким образом, математическая модель данной задачи можно сформулировать следующим образом.
Найти минимум целевой функции
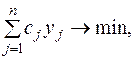 (5)
(5)
при ограничениях
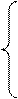
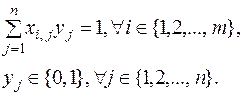 (6)
(6)
Целевая функция (5) представляет собой общую величину транспортных затрат на обслуживание заказов всех клиентов. Первое ограничение в (6) гарантируют обслуживание каждого заказа лишь одним исполнителем (маршрутом), т.е. заказы клиентов не должны разбиваться между двумя и более маршрутами. Условия двоичности переменных 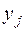 выражены во втором ограничении. В математической постановке задачи о назначениях (5)-(6) переменные
выражены во втором ограничении. В математической постановке задачи о назначениях (5)-(6) переменные 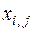 являются коэффициентами в системе ограничений, наряду с
являются коэффициентами в системе ограничений, наряду с 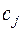 , являющимися коэффициентами целевой функции. Переменными в данной модели являются только
, являющимися коэффициентами целевой функции. Переменными в данной модели являются только 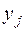 .
.
 2015-06-24
2015-06-24 367
367








