Раздел III. Образец решения задачи

1. Рассмотрим решение задачи на примере. Возьмем следующую таблицу данных:

Номер интервала	Интервал интенсивности потребления	Частота

2. Выделите в таблице столбец Частота и перетащите его вправо, чтобы образовался пустой столбец. Озаглавьте новый столбец Середины интервалов. Рассчитайте середины интервалов интенсивности потребления 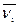по формуле

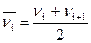. (1)

3. Построим гистограмму частот спроса на тару. Выделите в таблице столбцы Середины интервалов и Частота, щелкните на панели инструментов кнопку Мастер диаграмм (или найдите в меню Вставка), на вкладке Стандартные выберите тип Гистограмма, в правом окошке щелкните гистограмму в левом верхнем углу, нажмите Далее. Перейдите на вкладку Ряд, в окошке Ряд щелкните Середины интервалов, нажмите кнопку Удалить, нажмите Далее.

На вкладке Заголовки в окошке Название диаграммы наберите Частоты. На вкладке Таблица данных рядом с надписью Таблица данных поставьте флажок. На вкладке Подписи данных поставьте флажок рядом с надписью Значения. На вкладке Линии сетки в разделе Ось Y (значения) снимите флажок Основные линии. На вкладке Легенда снимите флажок Добавить легенду. Нажмите кнопку Далее, затем кнопку Готово.

Разместите гистограмму ниже таблиц. Откорректируйте ее - щелкните правой кнопкой по столбцам гистограммы, выберите Формат рядов данных, на вкладке Параметры установите ширину зазора равной 0. Нажмите ОК. Разместите готовую гистограмму ниже таблицы. Гистограмма должна иметь следующий вид:

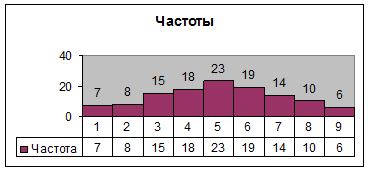
4. По виду гистограммы можно выдвинуть гипотезу о нормальном законе распределения спроса. Проверим гипотезу, применив критерий Пирсона. Необходимо найти математическое ожидание спроса по формуле

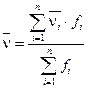, (2)

где n – число интервалов группировки, 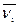– середина i-го интервала, f_i – частота i-го интервала.

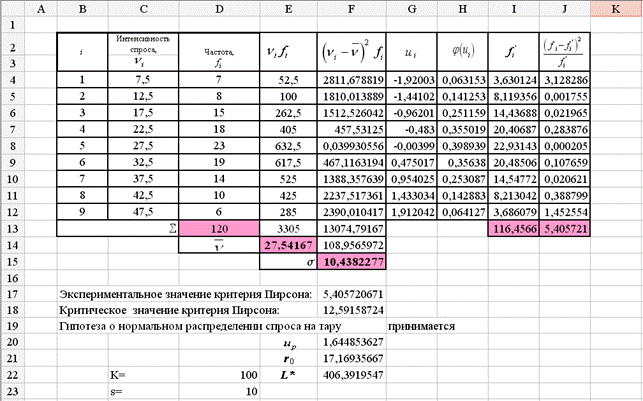
Вычисления по формуле (2) лучше всего проводить пошагово. Добавьте в таблицу строки и столбцы, как указано в образце:

Номер интервала	Интервал интенсивности потребления	Середины интервалов	Частота	Произведения середин интервалов и частот
			7,5
			12,5
			17,5
			22,5
			27,5
			32,5
			37,5
			42,5
			47,5
			суммы
				мат. ожидание

1) Найдите 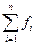- сумму значений в столбце Частоты.

2) В столбце Произведения середин интервалов и частот найдите все произведения вида 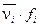(середины интервалов умножаются на частоты) и просуммируйте их (это будет значение 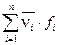). Вычислите математическое ожидание по формуле (2).

5. Теперь нужно рассчитать среднеквадратическое отклонение случайной величины спроса по формуле:

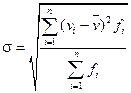. (3)

Добавьте в таблицу новые столбцы: Разность (середина интервала – мат. ожидание), Квадрат разности и Произведение квадрата разности и частоты. Рассчитайте указанные величины для каждой строки таблицы. Просуммируйте значения в последнем столбце (получится величина 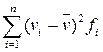), затем разделите ее на сумму частот и вычислите корень. Эта часть таблицы будет выглядеть следующим образом:

Разность (середина интервала – мат. ожидание)	Квадрат разности	Произведение квадрата разности и частоты
-20,041667	401,6684	2811,679
-15,041667	226,25174	1810,014
-10,041667	100,83507	1512,526
-5,0416667	25,418403	457,5313
-0,0416667	0,0017361	0,039931
4,95833333	24,585069	467,1163
9,95833333	99,168403	1388,358
14,9583333	223,75174	2237,517
19,9583333	398,33507	2390,01
		13074,79
	Среднее квадратическое отклонение	10,43823

6. Добавьте в таблицу столбец Нормализация и рассчитайте для каждой строки значения u_i с помощью функции НОРМАЛИЗАЦИЯ. Первый параметр — середина интервала, второй — мат. ожидание, третий – среднеквадратическое отклонение (т.к. 2-й и 3-й параметры меняться не будут, то можно использовать абсолютные ссылки со знаком $).

7. Следующий столбец назовите Нормрасп и рассчитайте для каждой строки значения j(u) (плотность распределения), используя функцию НОРМРАСП. Первый параметр – значение из столбца Нормализация, второй – 0, третий – 1, четвертый – ЛОЖЬ.

8. В столбце Теоретическая частота рассчитайте частоты f_i ^` по формуле

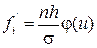, (4)

учитывая, что n – количество наблюдений (сумма значений столбца Частота), h – длина шага между соседними значениями спроса, σ – среднеквадратическое отклонение, j(u) – значения из столбца Нормрасп.

9. В столбце Критерий Пирсона вычислите величины 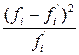, где f_i – частоты, f_i ' – теоретические частоты. В строке Суммы сделайте отдельный заголовок:

значение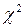

и найдите наблюдаемое значение критерия Пирсона по формуле

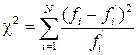. (5)

Примечание: все дальнейшие вычисления можно располагать столбиком:

значение	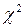5,405721
критическое значение
up
страховой запас

10. С помощью функции ХИ2ОБР найдите критическое значение критерия Пирсона 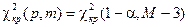, где α – заданный коэффициент надежности, M – число групп. Если 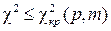, то выдвинутая гипотеза принимается, в противном случае – отвергается. Сделайте содержательный вывод о гипотезе.

Для примера получаем c² _набл = 5,4; c² _крит (1–α, M–3) = c² _крит (0,05; 6) = 12,59.

Вывод: так как наблюдаемое значение меньше критического, то гипотеза о нормальном законе распределения спроса подтверждается.

11. Величину u_p находим, используя функцию НОРМСТОБР. Введём уровень надёжности, равный по условию 0,95, получим, что u_p = 1,6448.

Страховой запас рассчитаем по формуле

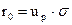. (6)

Итак, получены следующие значения:

значение	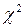5,405721
критическое значение	12,59158
up	1,644853
страховой запас	17,16936

12. Вычислите минимальные издержки работы системы по формуле

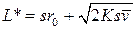, (7)

где K – затраты на организацию заказа, s – стоимость хранения одной единицы заказа, r₀ – страховой запас, 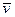- средняя интенсивность спроса (мат. ожидание).