Представление чисел в различных системах счисления

Арифметические основы цифровой техники.

СИСТЕМЫ СЧИСЛЕНИЯ.

Представление чисел в различных системах счисления.

Для преставления в цифровых устройствах чисел, а также другой информации в процессе программирования наряду с привычной для нас десятичной системой счисления широко используются другие системы. Рассмотрим наиболее употребительные позиционные системы счисления. Числа в таких системах счисления представляются последовательностью цифр (цифр разрядов), разделенных запятой на две группы: группу разрядов, изображающую целую часть числа, и группу разрядов, изображающую дробную часть числа:

… , , …

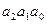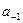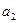Здесь 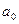, , 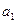…обозначают цифры нулевого, первого и т.д. разрядов целой части числа, 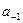, 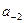… - цифры первого, второго и т.д. разрядов дробной части числа.

Цифре разряда приписан вес 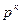, где 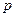– основание системы счисления; 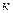– номер разряда, равный индексу при обозначениях цифр разрядов. Так, приведенная выше запись означает следующее количество:

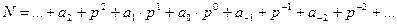
Для представления цифр разрядов используется набор из 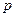различных символов. Так, при 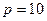(т.е. в обычной десятичной системе счисления) для записи цифр разрядов используется набор из десяти символов: 0, 1, 2, …, 9. При этом запись 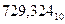(здесь и далее индекс и при числе указывает основание системы счисления, в которой представлено число) означает следующее количество:

,

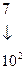
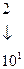
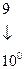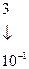
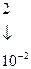
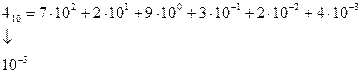
Весовые коэффициенты разрядов

Используя такой принцип представления чисел, но выбирая различные значения основания р, можно строить разнообразные системы счисления.

В двоичной системе счисления основание системы счисления р = 2. Таким образом, для записи цифр разрядов требуется набор всего лишь из двух символов, в качестве которых используются 0 и 1. Следовательно, в двоичной системе счисления представляется последовательностью символов 0 и 1. При этом запись 11011,1012 соответствует в десятичной системе счисления следующему числу:

,

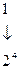
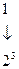
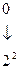
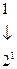
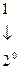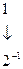
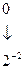
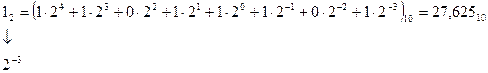
Весовые коэффициенты разрядов

В восьмеричной системе счисления основание системы счисления р = 8. Следовательно, для представления цифр разрядов должно использоваться восемь разных символов, в качестве которых выбраны 0, 1, 2, …, 7 (заметим, что символы 8 и 9 здесь не используются и в записи чисел встречаться не должны). Например, записи 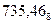в десятичной системе счисления соответствует следующее число:

,

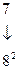
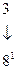
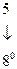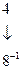
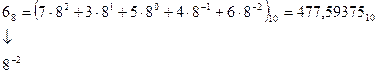
Весовые коэффициенты

разрядов

т.е. запись 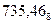означает число, содержащее семь раз по 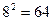, три раза по 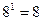, пять раз по 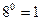, четыре раза по 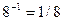, шесть раз по .

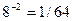В шестнадцатеричной системе счисления основание системы счисления р = 16 и для записи цифр разрядов должен использоваться набор из 16 символов: 0, 1, 2, …, 9, А, B, C, D, E, F. В нем используются 10 арабских цифр, и до требуемых шестнадцати их дополняют шестью начальными буквами латинского алфавита. При этом символу А в десятичной системе счисления соответствуют 10, B – 11, C – 12, D – 13, E – 14, F – 15.

Запись 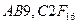соответствует следующему числу в десятичной системе счисления:

,

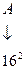
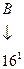
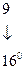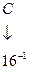
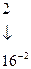
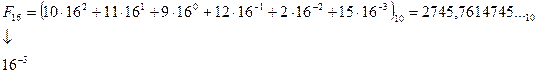
Весовые коэффициенты разрядов

Для хранения n -разрядных чисел в цифровой аппаратуре можно использовать устройства, содержащие n элементов, каждый из которых запоминает цифру соответствующего разряда числа. Наиболее просто осуществляется хранение чисел, представленных в двоичной системе счисления. Для запоминания цифры каждого разряда двоичного числа могут использовать устройства с двумя устойчивыми состояниями (например, триггеры). Одному из этих устойчивых состояний ставится в соответствие цифра 0, другому – цифра 1.

При хранении десятичных чисел каждая цифра десятичного числа представляется в двоичной форме. Такая форма представления чисел называется двоично-кодированной десятичной системой. Например, число 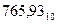в двоично-кодированной десятичной системе представляется в следующем виде:

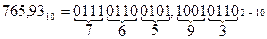
Следует заметить, что несмотря на внешнее сходство двоично-кодированного десятичного числа, содержащего в разрядах лишь цифры 0 и 1, с двоичным числом, первое не является двоичным. В этом легко убедиться. Например, если целую часть приведенной выше записи рассматривать как двоичное число, то оно при переводе в десятичную форму означало бы 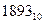, что не совпадает с целой частью исходного числа 765.

Рассмотренный способ двоичного представления (кодирования) десятичных цифр использует так называемый код 8421 (название кода составлено из весовых коэффициентов разрядов двоичного числа). Наряду с этим кодом при двоичном кодировании десятичных цифр используются различные другие коды, наиболее употребительные из которых приведены в табл. 2.1.

Таблица 2.1.

Десятичная цифра	Двоичное кодирование десятичной цифры
код8421	код2421	код 2 из 5	код с изб. 3	код За+2	код 7421

Код 7421 интересен тем, что любая кодовая комбинация содержит не более двух единиц. В коде 2 из 5 все кодовые комбинации содержат точно две единицы. Это свойство используется для обнаружения ошибочных комбинаций (ошибочное распознавание любого из символов принятой кодовой комбинации изменяет число единиц в этой комбинации).
Пары десятичных цифр, сумма которых равна девяти, составляют цифры, взаимно дополняющие друг друга до девяти (0 и 9, 1 и 8, 2 и 7,...). В коде 2421 и коде с избытком З кодовая комбинация, соответствующая любой из десятичных цифр, представляет собой инверсию комбинации, соответствующей ее дополнению до девяти. Например, в коде 2421 паре взаимно дополняющих до девяти цифр 2 и 7 соответствуют комбинации 0010 и 1101, каждая из которых образуется как инверсия другой. Это свойство упрощает выполнение в цифровых устройствах арифметических операций над десятичными числами. Таким же свойством дополнения до девяти обладает код 3а + 2. Кроме того, этот код имеет и другое полезное свойство: любая пара кодовых комбинаций отличается не менее, чем, а двух разрядах, что позволяет обнаруживать ошибочные комбинации (ошибка, изменяющая цифру одного разряда любой из кодовых комбинаций, приводит к так называемой запрещенной комбинации, не используемой для представления десятичных цифр в этом коде).

Преобразование чисел из одной системы счисления в другую

Основания восьмеричной и шестнадцатеричной систем счисления выражаются целой степенью двух (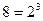, 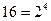). Этим объясняется простота преобразования чисел, представленных в этих системах счисления, в двоичную систему счисления и обратно.
Для перевода чисел из восьмеричной системы счисления в двоичную достаточно каждую цифру восьмеричного числа представить трехразрядным двоичным числом. Например,

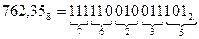
Перевод шестнадцатеричных чисел в двоичную систему счисления достигается представлением цифр шестнадцатеричного числа четырехразрядными двоичными числами. Например,

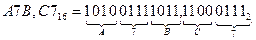
При обратном переводе чисел из двоичной системы в восьмеричную или шестнадцатеричную систему счисления необходимо разряды двоичного числа, отсчитывая их от запятой влево и вправо, разбить на группы по три разряда в случае перевода в восьмеричную систему или на группы по четыре разряда в случае перевода в шестнадцатеричную систему счисления. Неполные крайние группы дополняются нулями. Затем каждая двоичная группа представляется цифрой той системы счисления, в которую переводится число. Например,

;

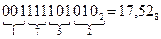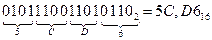
Большую сложность представляет перевод чисел из десятичной системы в двоичную и обратно. Метод такого перевода зависит от системы счисления, в которой проводятся арифметические операции, необходимые для перевода числа из одной системы счисления в другую. Если перевод осуществляется в ручную, то операции будут выполняться в десятичной системе счисления, если цифровым устройством – то в двоичной системе счисления. Рассмотрим эта два случая раздельно.

Перевод чисел с выполнением операций над десятичными числами. Так как перевести числа из двоичной системы в шестнадцатеричную и обратно нетрудно, то для простоты выкладок рассмотрим перевод чисел из шестнадцатеричной системы в десятичную и обратно.
В качестве примера перевода числа из шестнадцатеричной системы в десятичную систему выберем число 9А5F, С83В16. С учетом весов разрядов шестнадцатеричной системы счисления запишем это число в десятичной системе счисления:

+

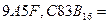
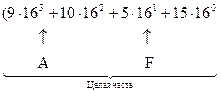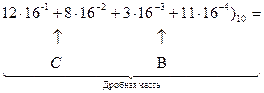
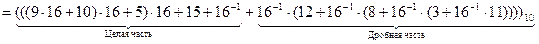
Здесь путем группировки членов вычисления полиномов представлено в форме так называемой схемой Горнера, обеспечивающей минимальной число выполняемых операций умножения.

Вычисления в приведенном примере дают следующий результат:

/

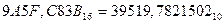Целая часть числа преобразуется точно, дробная часть – приближенно. При этом вычисления при нахождении дробной части выполнялись с точностью, определяемой семью десятичными разрядами.

Рассмотрим обратный перевод чисел из десятичной системы счисления в шестнадцатеричную. Воспользуемся приведенным выше примером. Теперь будем считать заданным число 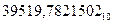и искать его представление в шестнадцатеричной системе счисления. Из равенства

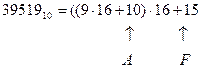
Можно вывести следующее правило получения цифр шестнадцатеричного представления. Деление правой части равенства (т.е. целой части заданного десятичного числа) на 16 дает частное 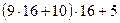и остаток 15 (т.е. F); деление полученного частного на 16 дает частное 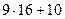и остаток 5; деление последнего частного на 16 приводит к частному 9 и остатку 10 (т.е. А). Таким образом, последовательно деля на 16 целую часть десятичного числа и образующиеся частные, получаем в последнем частном и остатках цифры всех разрядов шестнадцатеричного представления целой част числа.

Покажем эти действия по преобразованию десятичного числа 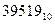в шестнадцатеричную систему счисления:

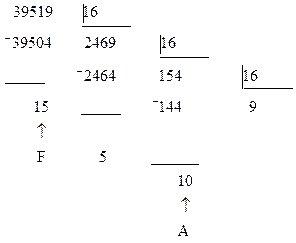
Отсюда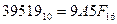

Теперь рассмотрим преобразование дробной части десятичного числа в шестнадцатеричную систему счисления. Из равенства

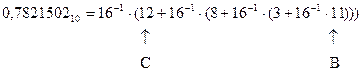
следует, что для получения цифр разрядов дробной части шестнадцатеричного числа 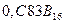необходимо последовательно умножать на 16 дробную часть исходного десятичного числа и дробные части образующихся произведений. При этом целые части этих произведений являются цифрами шестнадцатеричного представления:

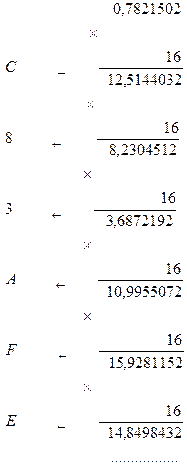
Таким образом, 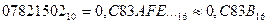. И в этом случае убеждаемся, что дробные числа преобразуется неточно.

Перевод чисел с выполнением операций в двоичной системе счисления. Рассмотрим перевод десятичных чисел в двоичную систему счисления. Для иллюстрации метода перевода выберем десятичное число 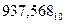, которое представим в следующей форме:

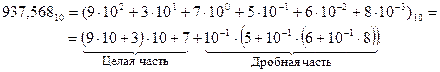
Представив числа, входящие в правую часть равенства, 4-разрядными двоичными числами, запишем выражения для преобразования целой и дробной частей:

,

.

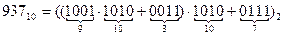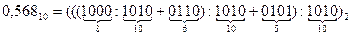Получаемые в результате выполнения операций над двоичными числами значения являются двоичными представлениями соответственно целой и дробной частей исходного числа.

Рассмотрим обратный перевод двоичных чисел в десятичную систему счисления. Перевод целых двоичных чисел производится последовательным делением в двоичной системе счисления на число 10102 исходного двоичного числа и всех образующихся частных. При этом последнее частное и возникающие при делении остатки являются двоичными представлениями цифр разрядов искомого десятичного представления числа.
Перевод дробной части двоичного числа производится последовательным умножением на двоичное число 10102 исходного числа и дробных частей получаемых произведений. При этом целые части произведений являются двоичным представлением цифр разрядов искомого десятичного представления дробного числа.
Некоторые правила, облегчающие обращение
с двоичными числами
1. Следует на память знать двоичные представления десятичных чисел от 0 до 15 (см. табл. 1.4).
2. Необходимо на память знать десятичные значения чисел 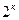от 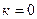(см. табл. 2.2).

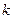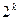3.Следует помнить следующие соотношения:

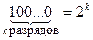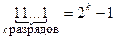а) , б) , в) .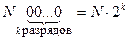

Эти соотношения в ряде случаев облегчают перевод двоичных чисел в десятичную систему счисления. Например,
г)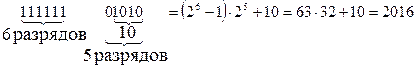

д)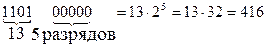

4.При чтении дробных двоичных чисел используются соотношения

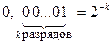
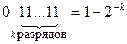
Например,

,

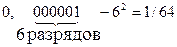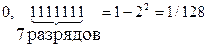
Знакоразрядная форма представления двоичных чисел.
В этой форме в разрядах числа допускается использование трех символов: 0,1 и 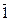(равный -1). Например,

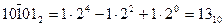
Знакоразрядная форма имеет следующие особенности:
а) представление чисел неоднозначно; например, приведенное выше число IЗ может быть представлено в следующих видах:

;

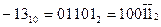б) исключается необходимость в знаковом разряде:

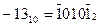
(при изменении знака числа достаточно изменить знак цифр разрядов);

в) возможна минимизация количества ненулевых разрядов.
Преобразование двоичных чисел в знакоразрядную форму с минимальным числом ненулевых разрядов осуществляется следующим образом. На первом этапе все встречающиеся в двоичном числе комбинации вида 01... 1 (при числе единиц в комбинации, большем одной) заменяются равнозначными комбинациями вида 10... 0 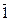с тем же числом разрядов. Эти преобразования продолжаются, пока не будут исключены все комбинации указанного вида. На следующем этапе комбинации видов 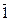1 и 1 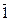заменяются соответственно комбинациями 01 и 0 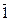. Покажем эти преобразования на примере:

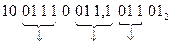
1-й этап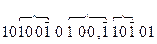

2-й этап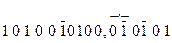

Как видим, количество ненулевых разрядов, равное в исходном числе 10, сократилось до 7. Сокращение числа ненулевых разрядов может существенно упростить и ускорить операцию умножения, так как сокращается количество суммируемых частичных произведений. Возможно ускорение и операции деления.

Упражнения
Над числами, представленными в вариантах а) — в):
а)5170,2368, А39,ЕВ416, 4037,58710, 1001111100,1101112,
б) 6304,3528, FВА,97516, З987,65410, 1011111000,1011102,
в)2736,5038,ЕFО,В9416,3095,74310, 1000111101,1101112,
проведите следующие операции:
1) преобразование восьмеричных чисел в двоичную систему счисления;
2) преобразование шестнадцатеричных чисел в двоичную систему счисления;
3) преобразование двоичных чисел в восьмеричную систему счисления;
4) преобразование двоичных чисел в шестнадцатеричную систему счисления;
5) преобразование восьмеричных чисел в десятичную систему счисления;
6) преобразование шестнадцатеричных чисел в десятичную систему счисления;
7) преобразование двоичных чисел в десятичную систему счисления;
8) преобразование десятичных чисел в шестнадцатеричную систему счисления;
9) представление двоичных чисел в знакоразрядной двоичной форме с минимальным числом ненулевых разрядов.
2.2. ФОРМЫ ПРЕДСТАВЛЕНИЯ ЧИСЕЛ
В ЦИФРОВЫХ УСТРОЙСТВАХ
Числа в цифровых устройствах могут представляться в форме целых чисел, чисел с фиксированной запятой и чисел с плавающей запятой.
Целые числа. При решении задач целые числа встречаются в случаях представления индексов переменных, подсчета числа повторений каких-либо действий и т. д. Для хранения целых чисел в ячейке памяти предусматривается распределение разрядов (разрядная сетка), показанное на рис. 2,1, а. Один из п разрядов отводится под знак числа, остальные разряды отводятся под модуль числа.
Обычно применяют следующий способ кодирования знака числа: “+“ обозначают цифрой 0 в знаковом разряде, “-“ — цифрой 1 в знаковом разряде.
Модуль числа занимает в разрядной сетке ее младшие разряды, свободные старшие разряды заполняются нулями. Например, число – 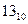, представленное в двоичной системе счисления значением 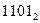, в 8-разрядной сетке имеет вид, показанный на рис. 2.1,б.

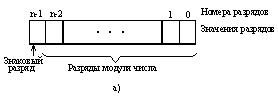
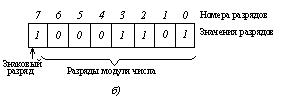
Рис.2.1.

Если количество значащих разрядов модуля числа, превышает 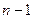, происходит потеря старших разрядов модуля. Это явление, называемое переполнением разрядной сетки, приводит к ошибке в представлении числа.
Диапазон модулей чисел, которые могут быть представлены в 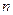-разрядной сетке, от 0 (при цифре 0 во всех разрядах модуля) до 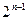(при цифре 1 во всех разрядах модуля).

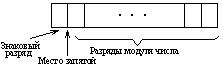
Рис. 2.2

В универсальных ЭВМ обычно используется два формата целых чисел: короткий с числом разрядов п = 16 и длинный п = 32. При этом максимальные значения модулей чисел соответственно

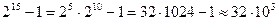(при п = 16);

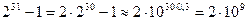(при п = 32)
Числа с фиксированной запятой. При этой форме обычно занятая, отделяющая целую часть числа от ее дробной части, фиксируется перед старшим разрядом модуля числа (рис. 2.2). Таким образом, значение модуля числа всегда оказывается меньше единицы. Это условие путем выбора определенных масштабных коэффициентов должно выполняться для исходных данных задачи и всех промежуточных результатов вычислений.

При занесении числа в ячейку памяти свободные младшие разряды модуля, которые поместились в разрядной сетке, теряются. Это приводит к погрешности, значение которой меньше единицы младшего разряда разрядной сетки, т.е. 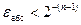. Так при п = 16 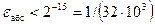, при п = 32 .

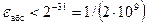Если число имеет целую часть, то для ее хранения в разрядной сетке места нет, она теряется, число в разрядной сетке оказывается ошибочным.

Достоинство представления чисел в форме с фиксированной запятой состоит в простате выполнения арифметических операций; недостатки – в необходимости выбора масштабных коэффициентов и в низкой точности представления чисел с малыми значениями модуля (нули в старших разрядах модуля приводит к уменьшению количества разрядов, занимаемых значащей частью модуля числа).

Числа с плавающей запятой. Для научно-технических расчетов необходимо представлять числа в широком диапазоне и с достаточно большой точностью. Указанным требованиям отвечают числа с плавающей запятой (рис.2.3).

Число состоит из мантиссы, старший разряд которой определяет знак числа, и порядка со знаком. Значение модуля мантиссы представляется двоичным дробным числом, т.е.

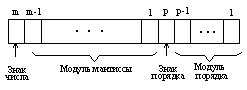
Рис.2.3

запятая фиксируется перед старшим разрядом модуля мантиссы, порядок представляется
целым числом. Порядок указывает действительное положение запятой в числе. Код
в приведенном формате представляет значение числа в полулогарифмической форме:
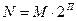Н = М 2, где М и П — мантисса и порядок числа.
Точность представления значений зависит от количества значащих цифр мантиссы. Для повышения точности числа с плавающей запятой представляются в нормализованной форме, при которой значение модуля мантиссы лежит в пределах 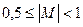. Признаком нормализованного числа служит наличие единицы в старшем разряде модуля мантиссы. В Нормализованной форме могут быть представлены все числа из некоторого диапазона за исключением нуля.
Нормализованные двоичные числа с плавающей запятой представляют значения модули чисел в диапазоне
,
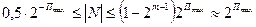где 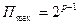— максимальное значение модуля порядка.
Так, при р = 7, 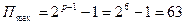и диапазон представления модулей нормализованных чисел

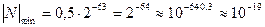
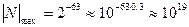
Таким образом, диапазон чисел от 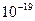до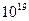
Для расширения диапазона представляемых чисел при фиксированной длине разряд- ной сетки 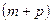в качестве основания системы счисления выбирается 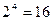. При этом число, представляемое а разрядной сетке, приобретает значение К = М 16”. Нормализованная мантисса 16-ричного числа с плавающей запятой имеет значение, лежащее в диапазоне 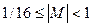Признаком нормализации такого числа является наличие хотя бы одной единицы в четырех старших разрядах модуля мантиссы. Диапазон представления чисел в этом случае существенно расширяется, находясь при том же количестве разрядов порядка в пределах от 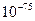до 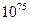. (Предлагается самостоятельно показать это).
Рассмотрим погрешность представления чисел с плавающей запятой. Абсолютная погрешность представления числа

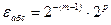
Предельная относительная погрешность — отношение абсолютной погрешности к числу при минимальном значении модули мантиссы нормализованного числа:
.
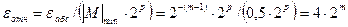Отсюда видно, что точность представления чисел определяется количеством разрядов, отводимых а разрядной сетке под мантиссу.
В современных ЭВМ числа с плавающей запятой имеют основание системы счисления 16 и представляются в двух форматах: коротком (с числом разрядов 32) и длинном (с числом разрядов 64). длинный формат предусматривает увеличение количества разрядов, отводимых в разрядной сетке под мантиссу, за счет чего повышается точность представления чисел.
Десятичные числа. Для кодирования десятичных чисел используются слова переменной длины с применением двух видов формата: упакованного и распакованного. Каждая десятичная цифра представляется двоичной тетрадой и занимает в разрядной сетке четыре разряда. Четыре разряда отводятся и для представления знака (собственно знак представляется младшим разрядом теграды, в остальных разрядах тетрады может использоваться постоянная комбинация 110).
При использовании упакованного формата каждый байт (8 разрядов двоичного числа) содержит две десятичные цифры (рис. 2.4,а).

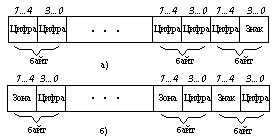
Рис.2.4

Например, число — 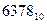представляется в упакованном формате в следующем виде:

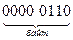
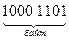
В распакованном формате каждый байт содержит лишь одну десятичную цифру в младшей тетраде; старшая тетрада, называемая зоной, заполняется стандартной комбинацией 1111 (рис. 2.4,б). Число — 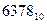представляется в этом формате в следующем виде:

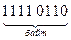
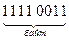
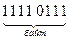
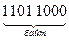
2.3. ВЫПОЛНЕНИЕ АРИФМЕТИЧЕСКИХ ОПЕРАЦИЙ
Основной операцией, которая используется в цифровых устройствах при различных вычислениях, является операция алгебраического сложения чисел (сложения, в котором могут участвовать как положительные, так и отрицательные числа). Вычитание легко сводится к сложению путем изменения на обратный знака вычитаемого. Операции умножения и деления также выполняются с помощью операции сложения и некоторых логических действий. Поэтому именно с операции сложения начнем рассмотрение способов выполнения арифметических операций.
При записи кода числа знак числа будем представлять полужирными цифрами О (для положительных чисел) и 1 (для отрицательных чисел). Положение запятой, отделяющей целую часть числа от дробной ее части, показывать не будем.
Сложение положительных двоичных чисел. Выполнение этой операции покажем на примере:

Переносы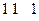

Первое слагаемое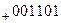

Второе слагаемое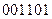

Сумма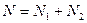

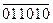
Цифры разрядов суммы формируются последовательно, начиная с младшего разряда. Цифра младшего разряда суммы образуется суммированием цифр младших разрядов слагаемых. При этом кроме цифры разряда суммы формируется цифра переноса в следующий, более старший разряд. Таким образом, в разрядах, начиная со второго, суммируются три цифры: цифры соответствующего разряда слагаемых и перенос, поступающий в данный разряд из предыдущего.
Перенос равен 1 во всех случаях, когда результат суммирования цифр в разряде равен или больше р = 2 (основание системы счисления). При этом в разряд суммы записывается цифра, нар единиц (т. е. на дне единицы) меньшая результата суммирования.

Алгебраическое сложение с использованием дополнительного кода. Для пояснения сущности излагаемого ниже метода рассмотрим следующий пример. Пусть требуется сложить два десятичных числа 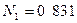и 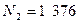. Так как второе слагаемое — отрицательное число, пользование приемом, излагаемым в школьной программе, потребовало бы последовательности действий с заемами из старших разрядов. Предусматривать в цифровом устройстве дополнительно такую последовательность действий не обязательно. Искомый результат может быть получен и при выполнении последовательности действий с передачей переносов в старшие разряды (как при сложении положительных чисел). Для этого достаточно отрицательное число 1 376 предварительно преобразовать в так называемый дополнительный код следующим образом: во всех разрядах, кроме знакового, запишем дополнение до 9 к цифрам этих разрядов и затем прибавим единицу в младший разряд. Число в дополнительном коде есть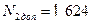
Далее произведем сложение по правилам сложения с передачей переносов в старшие разряды (т. е. так, как складываются положительные числа):

Переносы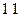

Первое слагаемое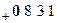

Второе слагаемое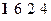

Сумма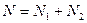

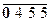
При сложении складываются и двоичные цифры знаковых разрядов с отбрасыванием возникающего из этого разряда переноса. Как видим, получен правильный результат (действительно, 831 – 376 = 455).

В двоичной системе счисления дополнительный код отрицательного числа формируется по следующему правилу: инвертируются (путем замены 0 на 1 и 1 на 0) цифры всех разрядов, кроме знакового, и в младший разряд прибавляется единица. Например, если 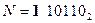, то 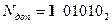. Обратное преобразование из дополнительного кода в прямой код производится по тому же правилу.
Рассмотрим примеры выполнения операции сложения.
Пример 2.1. Пусть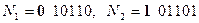

Переносы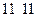

Первое слагаемое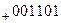

Второе слагаемое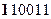

Сумма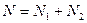

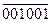
Как указывалось выше, перенос, возникающий из знакового разряда, отбрасывается.

Пример 2.2. Изменим на обратный знаки слагаемых (по отношению к предыдущему примеру) 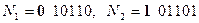. Очевидно, ожидаемый ответ .

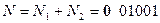Переносы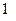

Первое слагаемое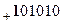

Второе слагаемое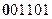

Сумма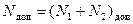

Сумма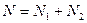

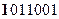
Таким образом, если результат сложения есть отрицательное число, то оно оказывается представленным в дополнительном коде.
Суммирование десятичных чисел. Вначале рассмотрим операцию суммирования в одном разряде десятичных чисел, т. е. суммирование двух десятичных цифр и единицы переноса, которая при суммировании чисел может поступить из предыдущего десятичного разряда. Способ суммирования десятичных цифр зависит от того, какой двоичный код выбран для представления десятичных цифр. Ниже рассматривается операция суммирования при использовании кода 8421.
Двоичные представления десятичных цифр суммируются по обычным правилам сложения двоичных чисел. Если полученная сумма содержит десять или более единиц, то формируется единица переноса, передаваемая в следующий десятичный разряд, а из суммы вычитаются десять единиц. Полученный результат есть цифра соответствующего разряда суммы. Наличие в полученной сумме десяти или более единиц выявляется по следующим признакам: появление переноса из разряда 8, возникающего при суммировании цифр; наличие единиц одновременно в разрядах 8 и 4 либо 8 и 2 в полученной сумме. При этом требуется коррекция суммы прибавлением к ней шести единиц (числа ).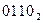
Покажем эти действия на примерах.
Пример 2.3. Сложить десятичные цифры 6 и 2 и перенос 1, поступающий из предыдущего десятичного разряда.

Десятичная система Код 8421

Переносы 1← 1 1 1

Первая цифра 6 0 1 1 0

Вторая цифра 2 0 0 1 0

Сумма

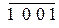
Коррекция −

Результат 1 0 0 0

В этом случае полученное в результате суммирования число 10012 меньше десяти и коррекция суммы не требуется.
Пример 2.4. Сложить десятичные цифры 8 и 9.

Десятичная система Код 8421

Переносы 1← 0← 1 0←

Первая цифра 8 1 0 0 0

Вторая цифра 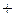9 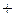1 0 0 1

Сумма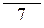

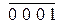
Коррекция 0 1 1 0

Результат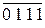

Как видно из примера, при выполнении умножения формируются частичные произведения (произведения множимого на цифры разрядов множителя), которые суммируются с соответствующими сдвигами относительно друг друга. В цифровых устройствах процессу суммирования частичных произведений придают последовательный характер:
формируется одно из частичных произведений, к нему с соответствующим сдвигом прибавляется следующее частичное произведение, к полученной сумме двух частичных произведений прибавляется с соответствующим сдвигом очередное частичное произведение, и так далее, пока не будут просуммированы все частичные произведения. Этот процесс суммирования можно начинать с младшего либо старшего частичного произведения.
Ниже показаны процессы при умножении с суммированием частичных произведений, начиная со старшего частичного произведения (используется приведенный выше пример
умножения чисел 11012 и 10112).

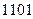4-е частичное произведение

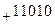сдвиг на один разрядов влево

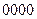3-е частичное произведение

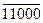сумма 4- и 3-го частичных произведений

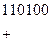сдвиг на один разряд влево

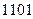2-е частичное произведение

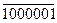сумма 4-, 3- и 2-гочастичных произведений

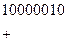сдвиг на один разряд влево

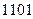1-е частичное произведение

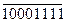произведение

Нетрудно убедиться, что при этом все частичные произведения суммируются с требуемыми сдвигами относительно друг друга, благодаря чему и образуется ранее приведенный результат умножения чисел.
При умножении целых чисел для фиксации произведения в разрядной сетке должно предусматриваться число разрядов, равное сумме числа разрядов множимого и множителя.
Рассмотрим подробнее выполнение данной операции.
На рис. 2. 5,а показана упрощенная схема множительного устройства. Здесь 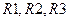— узлы; называемые регистрами. Каждый из них имеет некоторое число разрядов, которые могут устанавливаться в одно из двух состояний: 0 или 1. Таким образом, устанавливая разряды регистра в определенные состояния, можно обеспечить хранение в нем одного многоразрядного двоичного числа (более подробно о регистрах см. в § 2.7). На рисунке См — сумматор, суммирующий многоразрядные числа, поступающие на два его входа; Сч. - счетчик.
В регистр 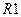поместим п- разрядное множимое. в регистр 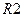n -разрядный множитель. В (п + 1)-разрядном регистре 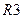будем накапливать сумму частичных произведений. Перед прибавлением к содержимому регистра Ю очередного частичного произведения хранящаяся в нем сумма предыдущих частичных произведений сдвигается вправо, и если очередное частичное произведение равно множимому, то См суммирует содержимое регистров 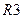и 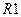, полученная сумма помещается в регистр 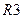. Таким образом к сумме предыдущих частичных произведений прибавляется очередное частичное произведение.

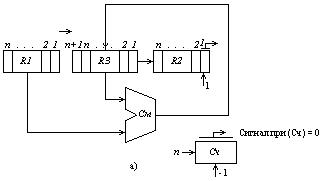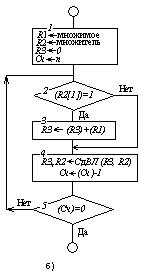Рис. 2.5

Одновременно со сдвигом содержимого регистра 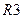сдвигается вправо и содержимое регистра 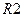. При каждом таком сдвиге в младший разряд регистра 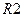поступает очередной разряд множителя, по которому определяется значение очередного частичного произведения (равное нулю или множимому). В освободившийся в результате сдвига старший разряд регистра 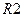можно принять выдвигаемый при сдвиге из регистра 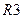младший разряд имеющегося в нем числа.
Подобные вычислительные процессы удобно описывать в форме так называемых схем алгоритмов. На рис. 2.5,бприведена схема алгоритма умножения. В блоке 1 показано исходное состояние регистров 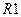, 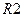; в регистре 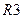устанавливается нулевое значение, в Сч помещается число n.

При построении схем алгоритмов для обозначения содержимого регистра наименование регистра заключается в круглые скобки (например, обозначение (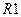) означает “содержимое регистра 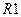”); для указания некоторого разряда регистра вслед за наименованием регистра в прямых скобках записывается номер разряда регистра (например, запись 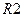[1] означает “1-й разряд регистра 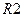”, ( 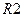[1]) “содержимое 1-го разряда регистра ”).
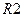Процесс умножения носит циклический характер. В блоке 2 проверяется значение младшего разряда числа в регистре 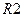( 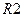[1]); если в нем содержится 1, то в блоке З к содержимому регистра 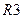прибавляется множимое, после чего производится сдвиг вправо содержимого регистров 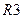и 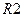; если в 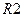[1) обнаруживается 0, частичное произведение равно нулю и блок суммирования обходится.

После n – кратного повторения этой группы действий в регистре 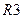образуется группа старших разрядов произведения, в регистре 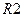— группа младших разрядов произведения. Для подсчета числа повторений этих действий предусмотрен счетчик Сч, в который предварительно (в блоке 1) помещается число п; далее после каждого повторения цикла из содержимого счетчика вычитается единица и проверяется, не равно ли нулю число в счетчике. В случае, если число в счетчике не достигло нулевого значения, производится повторение действий в цикле, при нулевом значении числа в счетчике происходит прекращение действий (выход из цикла).
Рассмотрим выполнение операции умножения с суммированием частичных произведений, начиная с младшего частичного произведения, на примере умножения дробных чисел 0,11012 и 0,10112.

Если требуется сохранить все разряды в произведении, то в устройстве, формирующем произведение, необходимо иметь число разрядов, равное сумме числа разрядов множимого и множителя. При умножении дробных чисел часто в произведении требуется сохранять то же число разрядов, что и в множимом. В таком приближенном представлении результата не фиксируются цифры разрядов, при сдвигах выдвигаемые правее показанной в примере вертикальной линии. Таким образом, цифры четырех младших разрядов в примере окажутся потерянными и будет получен приближенный результат 0,1000. Может быть проведено округление по правилу: если старший из отбрасываемых разрядов содержит единицу, то к младшему из сохраняемых разрядов прибавляется единица (результат с округлением равен в примере 0,1001).
При рассмотренном выше способе умножения выполнялись отделение от сомножителей их знаковых разрядов и раздельные действия над знаками и модулями чисел. Одним из эффективных алгоритмов умножения является алгоритм Бута. Он не предусматривает раздельных операций над знаковыми разрядами и модулями сомножителей. По этому алгоритму в результате образуется произведение со знаковым разрядом.
На рис. 2.6, а показана упрощенная схема устройства, выполняющего умножение с использованием алгоритма Буга. В регистры R1 и R2 предварительно помещаются множимое и множитель. В регистре R3 формируются старшие разряды произведения. В процессе выполнения операции по мере сдвига содержимого R2 вправо освобождающиеся старшие разряды заполняются младшими разрядами произведения; Т1 и Т2 — триггеры, хранящие одноразрядные двоичные числа (0 или 1). Счетчик предназначен для подсчета числа повторений цикла.
Процесс выполнения операции умножения на рис. 2.6,б представлен в форме схемы алгоритма. В блоке 1 в регистры R1 и R2 принимаются множимое и множитель, регистр R3, триггеры Т2 и Т1 устанавливаются в нулевое состояние, в счетчик заносится n — число

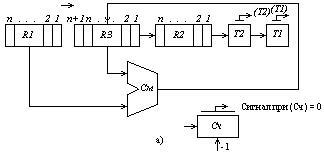
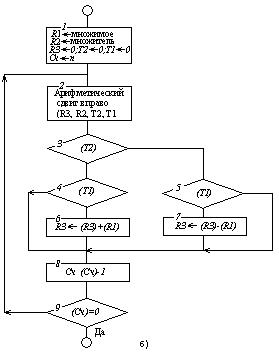
Рис. 2.6
разрядов в сомножителях (равное числу повторений цикла). В блоке 2 производится арифметический сдвиг содержимого регистров аз, R2 (при арифметическом сдвиге вправо в регистре R З сохраняется неизменным содержимое знакового разряда), рассматриваемого как единое число, в котором содержимое Ю образует его старшие разряды, содержимое R 2 — младшие разряды. Значение выдвигаемого из регистра младшего разряда принимается в Т2, хранившееся в Т2 значение передается в Т1. Таким образом, в Т2 и Т1 образуется последняя выдвинутая из R 2 пара разрядов множителя. В блоках З — 7 в зависимости от значений, образующихся в Т2и Т1, выполняются действия, показанные в таблице на с.92.

(Т2)	(Т1)	Выполняемые действия
		–
		Суммирование R3←(R3)+(R1)
		Вычитание R3←(R3) – (R1)
		–

В последующих блоках производится подготовка к повторению цикла. Содержимое счетчика уменьшается на единицу, и по результату проверки содержимого счетчика на нуль выясняется необходимость повторения цикла.

После выхода из цикла в R3 образуется знаковый разряд и группа старших разрядов произведения, а в (n -1) разрядах R2 – группа младших разрядов произведения.

Следует отметить, что отрицательные сомножители должны представляться в дополнительном коде, в этом же коде оказывается представленным произведение.

Рассмотрим пример умножения чисел 0 10112 (1110) и 1 11012(-1310). Дополнительный код второго числа 1 0011. Проводимые при умножении действия иллюстрируется табл. 2.3.

Деление двоичных чисел. При алгебраическом делении чисел выполняются действия по определению знака частного и действия по определению модуля частного. Знак частного может быть найден тем же способом, что и знак произведения в рассмотренной выше операции умножения с отделением знаковых разрядов. Поэтому опишем далее лишь нахождение модуля частного.

Таблица 2.3

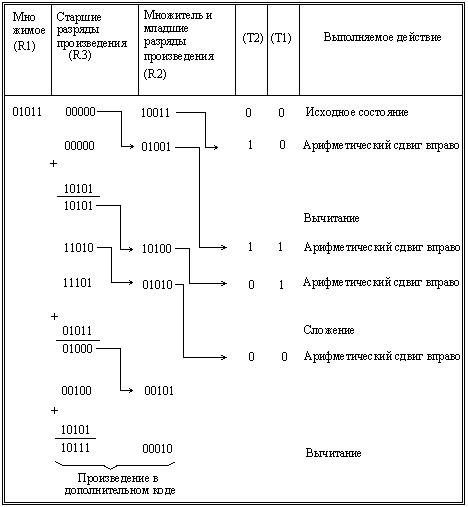
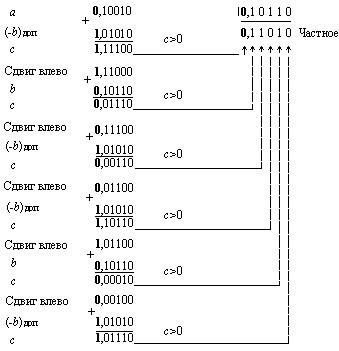
Пусть после отделения знаковых разрядов модули делимого и делителя представляются соответственно числами а = 0,10010 и b = 0,10110. встречающуюся в алгоритме операцию вычитания числа b заменим прибавлением – b, представленного в дополнительном коде: (- b)доп=1,01010

Умножение десятичных чисел. Рассмотрим процесс умножения на пример. Пусть перемножаются числа А = –75 и В = –23. Определив отдельно знак произведения так, как это производилось при умножении двоичных чисел (сложением по модулю 2 знаковых разрядов сомножителей), будем затем умножать модули чисел |А| = 75 и |В| = 23:

Процессы в множительном устройстве, связанные с выполнением этих действий, представлены в табл. 2.4.

Таблица 2.4

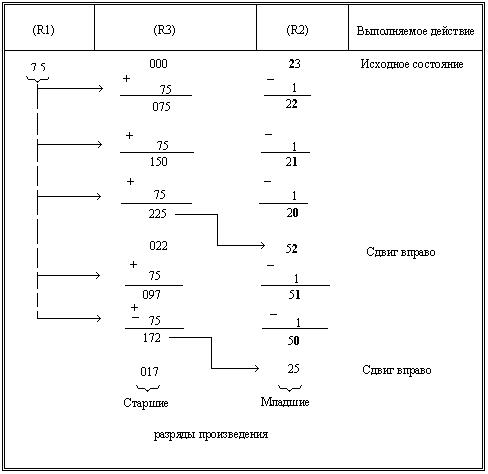
Пусть в регистрах R1 и R2 содержатся соответственно модули множимого (| А |=75) и множителя (| В |=23). Для накопления суммы частичных произведений используем регистр R3 с числом десятичных разрядов, на единицу большим числа разрядов в регистрах R1 и R2.

Для получения 1-го частичного произведения – произведения множимого на 1-й разряд множителя (75·3=225) будем суммировать множимое столько раз, сколько единиц содержится в 1-м разряде множителя (в таблице выделен полужирным шрифтом). Это можно выделить следующим образом. Предварительно установим в регистре R3 нулевое значение. Далее будем анализировать значение 1-го разряда регистра множителя R2. Если значение цифры в этом разряде не ровно нулю, прибавим множимое к содержимому регистра R3 и вычтем единицу из содержимого 1-го разряда регистра R2. Эти действия будем повторять до тех пор, пока в 1-м разряде регистра R2 не окажется нуль. К этому моменту в регистре R3 будет сформировано 1-е частичное произведение. Далее сдвинем содержимое регистров R3 и R2 на один десятичный разряд вправо так, чтобы выдвигаемая из регистра R3 десятичная цифра заняла освобождающийся в регистре R2 старший разряд.

Затем аналогично описанному в регистре R3 производятся накопление следующего частичного произведения и сдвиг вправо содержимого регистров R3 и R2. В регистре R3 образуются старшие разряды произведения, в регистре R2 – младшие разряды произведения.

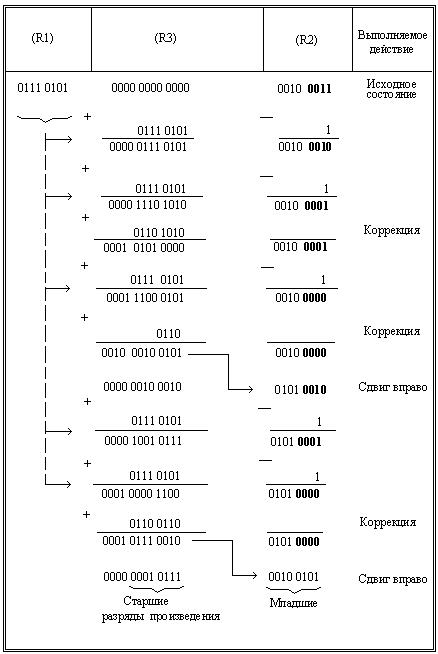
В табл. 2.5 показан тот же процесс умножения с представлением десятичных чисел в коде 8421 (т.е. с представлением чисел в двоично – кодированной десятичной системе счисления). Именно такая форма обычно используется в цифровых устройствах. Особенность показанных здесь действий состоит в том, что при суммировании в тетрадах регистра R3 могут возникать значения, превосходящие 10012(910). В этих случаях необходима коррекция с прибавлением в эти тетрады числа 01102(610). Кроме того, сдвигу на один десятичный разряд соответствует сдвиг на одну тетраду (на четыре двоичных разряда).

Деление десятичных цифр. Пусть участвующие в операции деления числа представлены в форме с фиксированной запятой и модуль делимого меньше модуля делителя (в противном случае результат операции – частное – окажется представленным с переполнением разрядной сетки). При делении знак частного определяется так же, как и при умножении – суммированием по модулю 2 значений знаковых разрядов делимого и делителя. Модуль частного находится делением модулей делимого и делителя. Эту операцию деления модулей чисел и будем рассматривать далее.

Делимое сдвигается на один десятичный разряд влево. Из него вычитается делитель. Если получающийся остаток положителен, в младший разряд регистра частного прибавляется единица. Эти действия (вычитание делителя и прибавление в разряд частного единицы) продолжаются до изменения знака остатка (до получения отрицательного остатка).

С появлением отрицательного остатка производится сдвиг влево остатка и содержимого регистра частного, после чего в младший разряд регистра частного записывается цифра 9. Далее выполняется серия прибавлений делителя к образующимся остаткам и вычитания из младшего разряда регистра частного единицы. Эти действия продолжаются до тех пор, пока не произойдет очередное изменение знака остатка (остаток не станет положительным). При этом после сдвига остатка прибавлением единицы содержимому младшего разряда регистра частного. Действия продолжаются до образования отрицательного остатка и т.д.

Проиллюстрируем правило деления на примере получения частного от деления чисел А = 0,159, В = 0,565. Для лучшего понимания действий, связанных с выполнением деления, используем обычное представление чисел в десятичной системе счисления.

Сдвиг влево	1,59	частное
Вычитание	0,565 ¯¯¯¯
Остаток	1,025	0,001
Вычитание	¯ 0,565 ¯¯¯¯
Остаток	0,460	0,002
Вычитание	¯ 0,565 ¯¯¯¯
Остаток	-0,105
Сдвиг влево	-1,050 +	0,029
Сложение	0,565 ¯¯¯¯
Остаток	-0,485 +	0,028
Сложение	0,565 ¯¯¯¯
Остаток	0,080
Сдвиг влево	0,800	0,280
Вычитание	¯ 0,565 ¯¯¯¯
Остаток	0,235	0,281